Trong mặt phẳng tọa độ, cho tam giác ABC, với A(6; – 2), B(4; 2), C(5; –5). Viết phương trình đường tròn ngoại tiếp tam giác đó.
Câu hỏi :
Trong mặt phẳng tọa độ, cho tam giác ABC, với A(6; – 2), B(4; 2), C(5; –5). Viết phương trình đường tròn ngoại tiếp tam giác đó.
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
Đường tròn ngoại tiếp tam giác ABC là đường tròn đi qua ba điểm A, B, C.
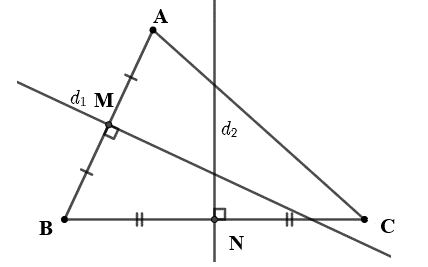
Các đoạn thẳng AB, BC tương ứng có trung điểm là M(5; 0), N\(\left( {\frac{9}{2};\,\,\frac{{ - 3}}{2}} \right)\).
Đường thẳng trung trực d1 của đoạn thẳng AB đi qua điểm M(5; 0) và có vectơ pháp tuyến \(\overrightarrow {AB} = \left( { - 2;\,4} \right)\).
Vì \(\overrightarrow {AB} = \left( { - 2;4} \right)\) cùng phương với \(\overrightarrow {{n_1}} = \left( {1;\, - 2} \right)\) nên d1 cũng nhận \(\overrightarrow {{n_1}} = \left( {1;\, - 2} \right)\) là vectơ pháp tuyến. Do đó, phương trình của d1 là: 1(x – 5) – 2(y – 0) = 0 hay x – 2y – 5 = 0.
Đường thẳng trung trực d2 của đoạn thẳng BC đi qua N\(\left( {\frac{9}{2};\,\,\frac{{ - 3}}{2}} \right)\) và có vectơ pháp tuyến \(\overrightarrow {BC} = \left( {1;\, - 7} \right)\), do đó phương trình d2 là: \(1\left( {x - \frac{9}{2}} \right) - 7\left( {y + \frac{3}{2}} \right) = 0\) hay x – 7y – 15 = 0.
Tâm I của đường tròn (C) ngoại tiếp tam giác ABC cách đều ba điểm A, B, C nên I là giao điểm của d1 và d2.
Vậy tọa độ của I là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - 2y - 5 = 0\\x - 7y - 15 = 0\end{array} \right.\).
Suy ra I(1; – 2). Đường tròn (C) có bán kính là IA =\(\sqrt {{{\left( {6 - 1} \right)}^2} + {{\left( { - 2 - \left( { - 2} \right)} \right)}^2}} = 5\).
Vậy phương trình của (C) là: (x – 1)2 + (y + 2)2 = 25.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Bài 21. Đường tròn trong mặt phẳng tọa độ có đáp án !!
Copyright © 2021 HOCTAP247
