Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục Oxy có gốc O là trung điểm của F1F2, tia Ox trùng tia OF2 (H.7.26). Nêu tọa độ của các tiêu điểm F1, F2. Giải...
Câu hỏi :
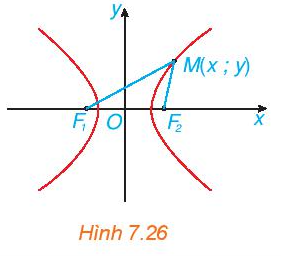
Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục Oxy có gốc O là trung điểm của F1F2, tia Ox trùng tia OF2 (H.7.26). Nêu tọa độ của các tiêu điểm F1, F2. Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi
. (3)
Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục Oxy có gốc O là trung điểm của F1F2, tia Ox trùng tia OF2 (H.7.26). Nêu tọa độ của các tiêu điểm F1, F2. Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi
. (3)

* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
+) Vì F1F2 = 2c, mà O là trung điểm của F1F2.
Do đó ta có: F1O = F2O = 2c : 2 = c.
Quan sát hình ta thấy, điểm F1 thuộc trục Ox, nằm bên trái điểm O và cách O một khoảng bằng F1O nên tọa độ F1(– c; 0).
Điểm F2 thuộc trục Ox, nằm bên phải điểm O và cách O một khoảng bằng F2O nên tọa độ F2(c; 0).
Vậy tọa độ các tiêu điểm: F1(– c; 0) và F2(c; 0).
+) Giả sử M(x; y) thuộc hypebol (H) ta cần chứng minh:
Thật vậy, M thuộc hypebol (H) nên: |MF1 – MF2| = 2a.
Lại có: MF1 = ;
MF2 =
⇒ |MF1 – MF2| =
Vậy .
+) Giả sử , ta cần chứng minh M thuộc hypebol (H).
Thật vậy: nên: |MF1 – MF2| = 2a.
Vậy M thuộc hypebol (H).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Bài 22. Ba đường conic có đáp án !!
Copyright © 2021 HOCTAP247
