Dự báo thời tiết trong ba ngày thứ Hai, thứ Ba, thứ Tư của tuần sau cho biết, trong mỗi ngày này, khả năng có mưa và không mưa như nhau. a) Vẽ sơ đồ hình cây mô tả không gian mẫu....

Hướng dẫn giải

a) Ta kí hiệu mưa là M và không mưa là KM.

Theo bài ra ta vẽ được sơ đồ hình cây mô tả không gian mẫu như sau:

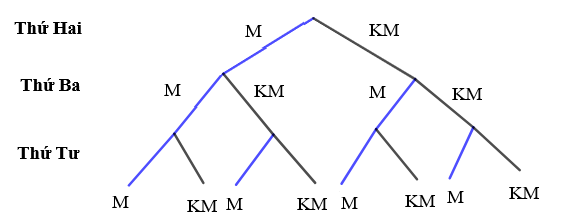
Do đó, Ω = {M – M – M; M – M – KM; M – KM – M; M – KM – KM; KM – M – M; KM – M – KM; KM – KM – M; KM – KM – KM}.

Vậy n(Ω) = 8.

b)

+ Biến cố F: “Trong ba ngày, có đúng một ngày có mưa”;

Theo sơ đồ ở câu a, ta có: F = {M – KM – KM; KM – M – KM; KM – KM – M}.

Do đó, n(F) = 3.

Vậy \(P\left( F \right) = \frac{{n\left( F \right)}}{{n\left( \Omega \right)}} = \frac{3}{8}.\)

+ Biến cố G: “Trong ba ngày, có ít nhất hai ngày không mưa”. (có 2 trường hợp, một là 2 ngày không mưa và hai là cả 3 ngày không mưa).

Theo sơ đồ ở câu a, ta có G = {M – KM – KM; KM – M – KM; KM – KM – M; KM – KM – KM}.

Do đó, n(G) = 4.

Vậy \(P\left( G \right) = \frac{{n\left( G \right)}}{{n\left( \Omega \right)}} = \frac{4}{8} = \frac{1}{2}.\)