Gieo một đồng xu cân đối liên tiếp bốn lần. a) Vẽ sơ đồ hình cây mô tả không gian mẫu. b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện m...

Hướng dẫn giải

a) Đồng xu cân đối nên các kết quả có thể là đồng khả năng.

Kí hiệu S và N tương ứng là đồng xu ra mặt sấp và đồng xu ra mặt ngửa.

Theo bài ra ta có sơ đồ hình cây mô tả không gian mẫu như sau:

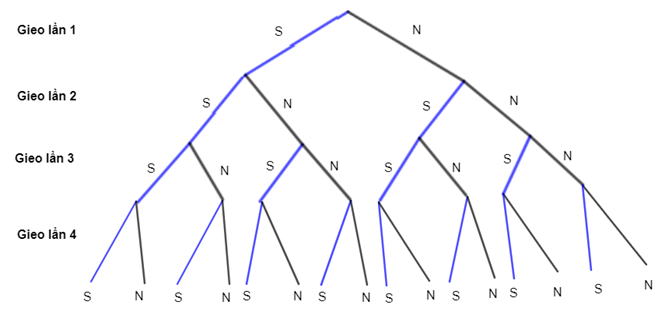
Do đó, n(Ω) = 16.

b) Gọi biến cố A: “Trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”.

Theo sơ đồ hình cây ở câu a, ta có:

A = {SSNN; SNSN; SNNS; NSSN; NSNS; NNSS}.

Do đó, n(A) = 6.

Vậy \(P\left( G \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{6}{{16}} = \frac{3}{8}.\)