Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét
Câu hỏi :
Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng bằng hàm số h(x) = - 0,1x2 + x – 1. Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ và ngang vành rổ? Làm tròn kết quả đến hàng phần mười.
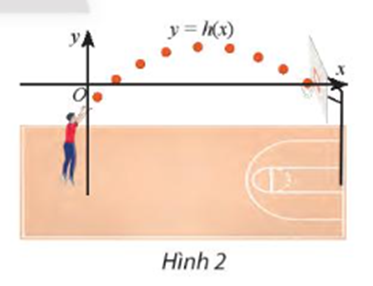
Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng bằng hàm số h(x) = - 0,1x2 + x – 1. Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ và ngang vành rổ? Làm tròn kết quả đến hàng phần mười.

* Đáp án
* Hướng dẫn giải
Ta có h(x) = -0,1x2 + x – 1 là tam thức bậc hai với a = -0,1, b = 1 và c = -1.
Tam thức bậc hai h(x) = -0,1x2 + x – 1 có ∆ = 12 – 4.(-0,1).(-1) = 0,6 > 0. Do đó h(x) có hai nghiệm phân biệt x1 = 5 + , x2 = 5 – và a = -0,1 < 0.
Ta có bảng xét dấu sau:
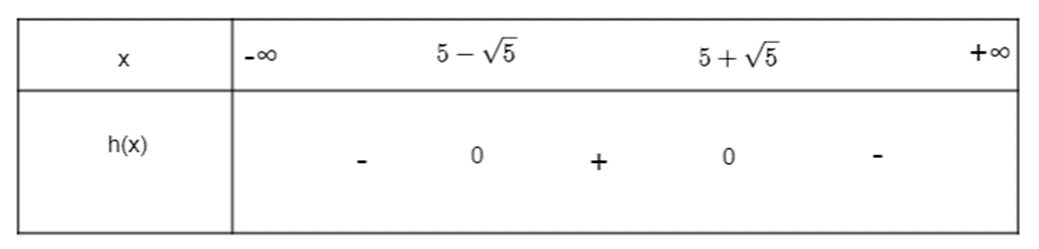
Suy ra h(x) dương khi x thuộc khoảng và h(x) âm khi x thuộc hai khoảng và .
Dựa vào hình vẽ ta thấy trục Ox chính là vành rổ.
Ta có và
Vậy với x thuộc khoảng (1,1; 8,9) thì bóng nằm cao hơn vành rổ và với x thuộc khoảng (– ∞;1,1) và (8,9 ; + ∞) thì bóng nằm thấp hơn vành rổ.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
