Một khung dây thép hình chữ nhật có chiều dài 20 cm và chiều rộng 15 cm được uốn lại
Câu hỏi :
Một khung dây thép hình chữ nhật có chiều dài 20 cm và chiều rộng 15 cm được uốn lại thành khung hình chữ nhật mới có kích thước (20 + x) cm và (15 – x) cm. Với x nằm trong các khoảng nào thì diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi?
Một khung dây thép hình chữ nhật có chiều dài 20 cm và chiều rộng 15 cm được uốn lại thành khung hình chữ nhật mới có kích thước (20 + x) cm và (15 – x) cm. Với x nằm trong các khoảng nào thì diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi?
* Đáp án
* Hướng dẫn giải
Diện tích khung dây thép hình chữ nhật ban đầu là: 20.15 = 300 (cm2).
Diện tích khung hình chữ nhật mới là: (20 + x)(15 – x) = 300 + 5x – x2 (cm2).
Xét hiệu f(x) = 300 – 300 – 5x + x2 = x2 – 5x.
Ta có f(x) = x2 – 35x là tam thức bậc hai có ∆ = (-35)2 – 4.1.0 = 1 225 > 0. Do đó h(x) có hai nghiệm phân biệt x1 = 0, x2 = -5 và a = 1 > 0.
Khi đó ta có bảng xét dấu:
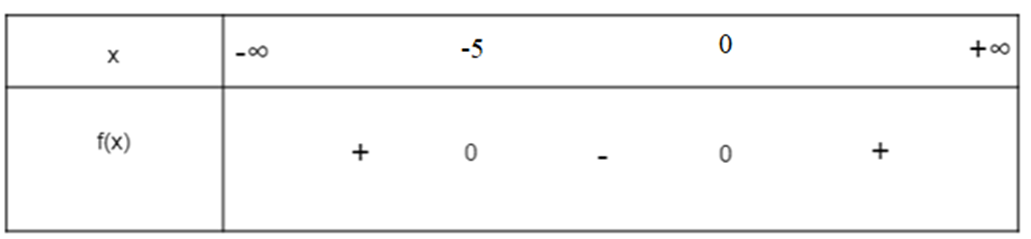
Suy ra f(x) âm khi x thuộc khoảng (-5; 0), f(x) dương khi x thuộc hai khoảng (-∞; -5) và (0; +∞).
Vậy với x thuộc khoảng (-5; 0) thì diện tích của khung dây thép tăng lên, x thuộc hai khoảng (-∞; -5) và (0; +∞) thì diện tích của khung dây thép giảm đi, và x = - 5 hoặc x = 0 thì diện tích khung dây thép không đổi.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
