Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án !!
Chứng minh rằng với mọi số thực m ta luôn...
Chứng minh rằng với mọi số thực m ta luôn có 9m^2 + 2m > - 3.
Câu hỏi :
Chứng minh rằng với mọi số thực m ta luôn có 9m2 + 2m > - 3.
Chứng minh rằng với mọi số thực m ta luôn có 9m2 + 2m > - 3.
* Đáp án
* Hướng dẫn giải
Ta có: 9m2 + 2m > - 3
⇔ 9m2 + 2m + 3 > 0
Đặt f(m) = 9m2 + 2m + 3
Ta thấy f(m) là tam thức bậc hai với a = 9, b = 2 và c = 3.
Ta có: ∆ = 22 – 4.9.3 = 4 – 108 = -104 < 0. Do đó f(m) vô nghiệm và a = 9 > 0.
Khi đó ta có bảng xét dấu:
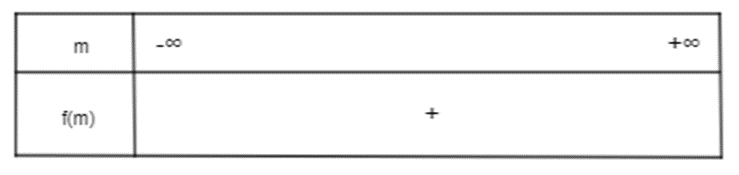
Từ bảng xét dấu ta thấy f(m) > 0 với mọi m
⇒ 9m2 + 2m + 3 > 0 với mọi m hay 9m2 + 2m > - 3 với mọi m.
Vậy 9m2 + 2m > - 3 với mọi m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án !!
Số câu hỏi: 15
Copyright © 2021 HOCTAP247
