Mặt cắt ngang của mặt đường thường có dạng hình parabol để nước mưa dễ dàng thoáng

Câu hỏi :

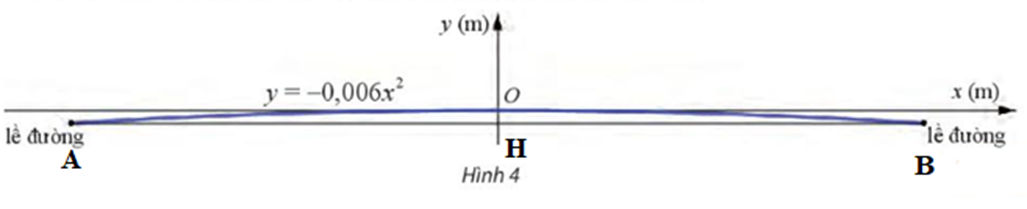
Mặt cắt ngang của mặt đường thường có dạng hình parabol để nước mưa dễ dàng thoáng sang hai bên. Mặt cắt ngang của một con đường được mô tả bằng hàm số y = - 0,006x² với gốc tọa độ đặt tại tim đường và đơn vị đo là mét như trong Hình 4. Với chiều rộng của đường như thế nào thì tim đường cao hơn lề đường không quá 15cm.

* Đáp án

* Hướng dẫn giải

Gọi A, H, B lần lượt là các điểm trên hình vẽ:

Đổi 15cm = 0,15 m

Để tim đường cao hơn lề đường không quá 15cm thì OH ≤ 0,15 hay – (– 0,006x²) ≤ 0,15

⇔ x² – 25 ≥ 0

Xét tam thức bậc hai f(x) = x² – 25 có ∆ = 0² – 4.(-25) = 100 > 0, a = 1 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ = - 5 và x₂ = 5.

Ta có bảng xét dấu:

Suy ra f(x) không âm khi x thuộc đoạn [-5; 5].

Tương ứng x₁, x₂ lần lượt là hoành độ của các điểm A và B. Khi đó AB = |x₂ – x₁| = |5 – (-5)| = 10.

Vậy độ rộng của đường là 10 m thì tim đường cao hơn lề đường không quá 15cm.