Trong hình bên, các tam giác vuông được xếp với nhau để tạo thành một đường tương
Câu hỏi :
Trong hình bên, các tam giác vuông được xếp với nhau để tạo thành một đường tương tự đường xoắn ốc. Với x bằng bao nhiêu thì OA = \(\frac{1}{2}\)OC?
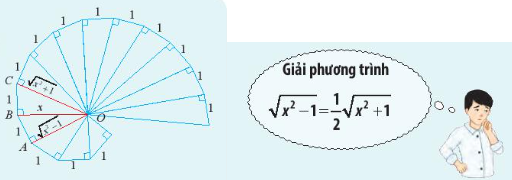
Trong hình bên, các tam giác vuông được xếp với nhau để tạo thành một đường tương tự đường xoắn ốc. Với x bằng bao nhiêu thì OA = \(\frac{1}{2}\)OC?

* Đáp án
* Hướng dẫn giải
Vì x là độ dài cạnh tam giác vuông nên x > 0.
Ta có OA = \(\frac{1}{2}\)OC
\( \Leftrightarrow \sqrt {{x^2} - 1} = \frac{1}{2}\sqrt {{x^2} + 1} \) (điều kiện x2 – 1 ≥ 0 ⇔ x2 ≥ 1 \( \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge 1\end{array} \right.\)).
\( \Leftrightarrow {x^2} - 1 = \frac{1}{4}\left( {{x^2} + 1} \right)\)
⇔ 4x2 – 4 = x2 + 1
⇔ 3x2 = 5
⇔ x2 = \(\frac{5}{3}\)
⇔ \(\left[ \begin{array}{l}{x_1} = - \sqrt {\frac{5}{3}} \\{x_2} = \sqrt {\frac{5}{3}} \end{array} \right.\)
Do đó x = \( - \sqrt {\frac{5}{3}} \)(không thỏa mãn) hoặc x = \(\sqrt {\frac{5}{3}} \)(thỏa mãn)
Vậy với x = \(\sqrt {\frac{5}{3}} \) thì OA = \(\frac{1}{2}\)OC.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Toán 10 Bài 3. Phương trình quy về phương trình bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
