Cho tam giác OAB và OBC lấn lượt vuông tại A và B như Hình 1. Các cạnh AB
Câu hỏi :
Cho tam giác OAB và OBC lấn lượt vuông tại A và B như Hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:
a) OC = 3OA;
b) OC = \(\frac{5}{4}\)OB.
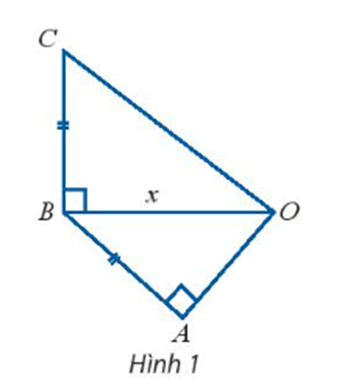
Cho tam giác OAB và OBC lấn lượt vuông tại A và B như Hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:
a) OC = 3OA;
b) OC = \(\frac{5}{4}\)OB.

* Đáp án
* Hướng dẫn giải
Ta có OB = x (cm)
Khi đó AB = BC = x – 1 (cm). Do đó x > 1
Xét tam giác OBC vuông tại B, có:
OC2 = OB2 + BC2 (định lí Py – ta – go)
⇔ OC2 = x2 + (x – 1)2 = 2x2 – 2x + 1
⇔ OC = \(\sqrt {2{x^2} - 2x + 1} \)
Xét tam giác OAB vuông tại A, có:
OB2 = AB2 + OA2 (định lí Py – ta – go)
⇔ OA2 = AB2 – OB2
⇔ OA2 = x2 – (x – 1)2 = x2 – (x2 – 2x + 1) = 2x – 1
⇔ OA = \(\sqrt {2x - 1} \)
a) Vì OC = 3OA nên \(\sqrt {2{x^2} - 2x + 1} \) = 3\(\sqrt {2x - 1} \)
⇒ 2x2 – 2x + 1 = 9(2x – 1)
⇒ 2x2 – 2x + 1 = 18x – 9
⇒ 2x2 – 20x + 10 = 0
⇒ x2 – 10x + 5 = 0
⇒ x = 5 + 2\(\sqrt 5 \) hoặc x = 5 – 2\(\sqrt 5 \).
Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy cả hai giá trị của x đều là nghiệm của phương trình đã cho. Tuy nhiên x = 5 – 2\(\sqrt 5 \)(không thỏa mãn x > 1)
Vậy với x = 5 + 2\(\sqrt 5 \)(cm) thì OC = 3OA.
b) Vì OC = \(\frac{5}{4}\)OB nên \(\sqrt {2{x^2} - 2x + 1} \) = \(\frac{5}{4}\)x
⇒ 2x2 – 2x + 1 = \(\frac{{25}}{{16}}\)x2
⇒ 16(2x2 – 2x + 1) = 25x2
⇒ 7x2 – 32x + 16 = 0
⇒ x = 4 hoặc x = \(\frac{4}{7}\).
Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy cả hai giá trị của x đều là nghiệm của phương trình đã cho. Tuy nhiên x = \(\frac{4}{7}\) (không thỏa mãn x > 1)
Vậy với x = 4 (cm) thì OC = \(\frac{5}{4}\)OB.Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Toán 10 Bài 3. Phương trình quy về phương trình bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
