Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một
Câu hỏi :
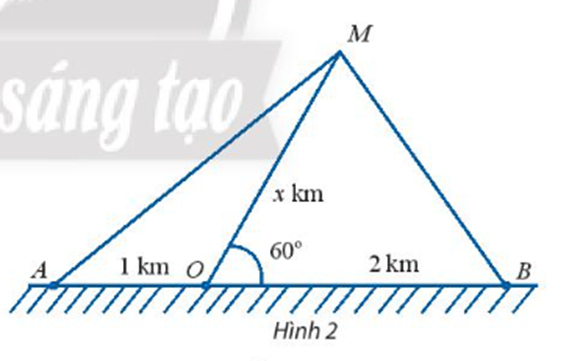
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc 60°. Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng cách 1km và 2km (Hình 2).
a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.
b) Tìm x để khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A.
c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500m.
Lưu ý: Làm tròn kết quả đến hàng phần trăm.
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc 60°. Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng cách 1km và 2km (Hình 2).
a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.
b) Tìm x để khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A.
c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500m.
Lưu ý: Làm tròn kết quả đến hàng phần trăm.

* Đáp án
* Hướng dẫn giải
a) Xét tam giác MOB có:
Áp dụng định lí côsin, ta có:
MB2 = OM2 + OB2 – 2.OM.OB.cos\(\widehat {BOM}\)
⇔ MB2 = x2 + 22 – 2.x.2.cos60°
⇔ MB2 = x2 + 4 – 2x
⇔ MB = \(\sqrt {{x^2} - 2x + 4} \) (km).
Ta lại có \(\widehat {AOM} + \widehat {BOM} = 180^\circ \) ⇒ \(\widehat {AOM} = 180^\circ - \widehat {BOM} = 180^\circ - 60^\circ = 120^\circ \).
Xét tam giác MOA có:
Áp dụng định lí côsin, ta có:
MA2 = OM2 + OA2 – 2.OM.OA.cos\(\widehat {AOM}\)
⇔ MA2 = x2 + 12 – 2.x.1.cos120°
⇔ MA2 = x2 + 1 + x
⇔ MA = \(\sqrt {{x^2} + x + 1} \) (km).
Vậy MA = \(\sqrt {{x^2} + x + 1} \) km và MB = \(\sqrt {{x^2} - 2x + 4} \) km.
b) Để khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A thì \(\sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \)
⇒ x2 – 2x + 4 = \(\frac{{16}}{{25}}\)(x2 + x + 1)
⇒ 25x2 – 50x + 100 = 16x2 + 16x + 16
⇒ 9x2 – 66x + 84 = 0
⇒ x = \(\frac{{11 - \sqrt {37} }}{3}\) hoặc x = \(\frac{{11 + \sqrt {37} }}{3}\).
Thay lần lượt các giá trị trên vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.
Vậy với x = \(\frac{{11 - \sqrt {37} }}{3}\) hoặc x = \(\frac{{11 + \sqrt {37} }}{3}\) thì khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A.
c) Đổi 500 m = 0,5 km = \(\frac{1}{2}\) km
Để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O 500 m thì
\(\sqrt {{x^2} - 2x + 4} = x - \frac{1}{2}\)
⇔ x2 – 2x + 4 = x2 – x + \(\frac{1}{4}\)
⇔ – x = \( - \frac{{15}}{4}\)
⇔ x = \(\frac{{15}}{4}\)
Vậy x = \(\frac{{15}}{4}\) thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O 500 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Toán 10 Bài 3. Phương trình quy về phương trình bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
