Xét dấu của các tam thức bậc hai sau: a) f(x) = 6x^2 + 41x + 44;
Câu hỏi :
Xét dấu của các tam thức bậc hai sau:
a) f(x) = 6x2 + 41x + 44;
b) g(x) = - 3x2 + x – 1;
c) h(x) = 9x2 + 12x + 4.
Xét dấu của các tam thức bậc hai sau:
a) f(x) = 6x2 + 41x + 44;
b) g(x) = - 3x2 + x – 1;
c) h(x) = 9x2 + 12x + 4.
* Đáp án
* Hướng dẫn giải
a) Tam thức bậc hai f(x) = 6x2 + 41x + 44 có ∆ = 412 – 4.6.44 = 625 > 0 và a = 6 > 0. Do đó f(x) có hai nghiệm phân biệt x1 = \( - \frac{4}{3}\) và x2 = \( - \frac{{11}}{2}\).
Khi đó ta có bảng xét dấu sau:
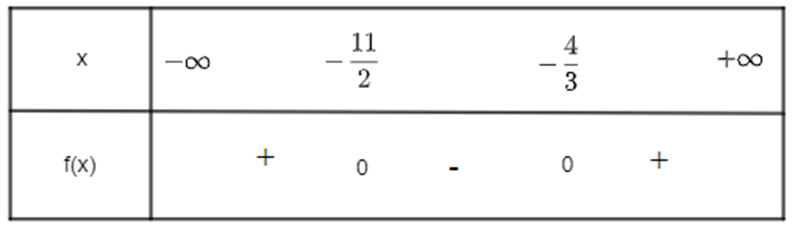
Vậy f(x) âm khi x thuộc khoảng \(\left( { - \frac{{11}}{2}; - \frac{4}{3}} \right)\), f(x) dương khi x thuộc hai khoảng \(\left( { - \infty ; - \frac{{11}}{2}} \right)\) và \(\left( { - \frac{4}{3}; + \infty } \right)\).
b) Tam thức bậc hai g(x) = - 3x2 + x – 1 có ∆ = 12 – 4.(-3).(-1) = -11 < 0 và a = -3 < 0. Do đó g(x) vô nghiệm. Khi đó ta có bảng xét dấu sau: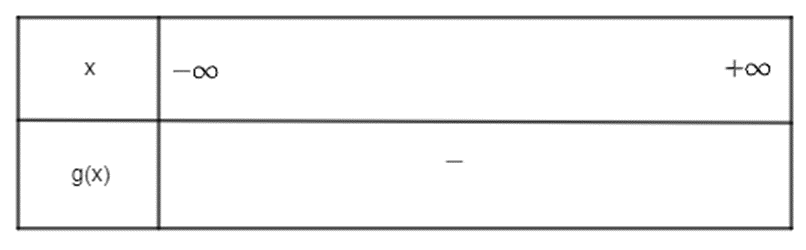
Vậy g(x) âm với mọi x ∈ ℝ.
c) Tam thức bậc hai h(x) = 9x2 + 12x + 4 có ∆ = 122 – 4.9.4 = 0 và a = 9 > 0. Do đó h(x) có nghiệm kép x1 = x2 = \(\frac{{ - 2}}{3}\).
Khi đó ta có bảng xét dấu sau:
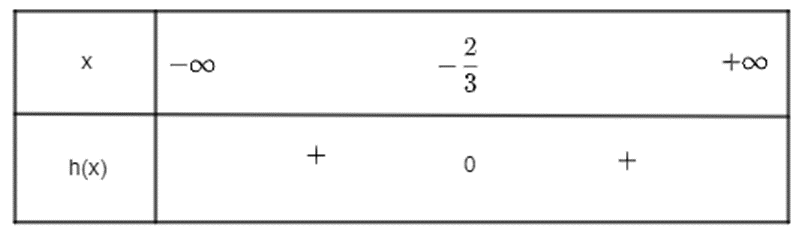
Vậy h(x) dương với mọi x ≠ \(\frac{{ - 2}}{3}\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Toán 10 Bài tập cuối chương 7 có đáp án !!
Copyright © 2021 HOCTAP247
