Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải thích các bất phương trình sau:
Câu hỏi :
Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải thích các bất phương trình sau:
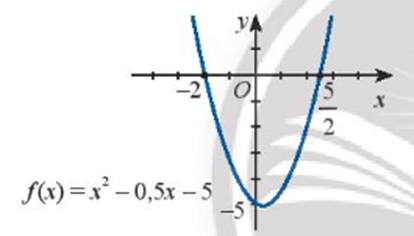
a) x2 – 0,5x – 5 ≤ 0
b) – 2x2 + x – 1 > 0
Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải thích các bất phương trình sau:
a) x2 – 0,5x – 5 ≤ 0

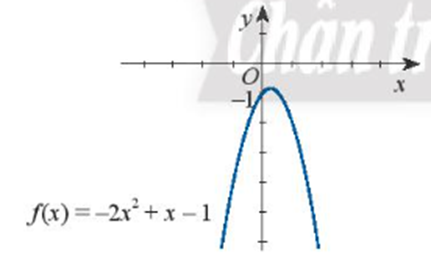
b) – 2x2 + x – 1 > 0

* Đáp án
* Hướng dẫn giải
a) Quan sát đồ thị ta thấy:
Với x thuộc hai khoảng (-∞; -2) và \(\left( {\frac{5}{2}; + \infty } \right)\) thì đồ thị hàm số nằm phía trên trục hoành. Do đó f(x) > 0 khi x ∈ (-∞; -2) ∪ \(\left( {\frac{5}{2}; + \infty } \right)\) .
Với x thuộc \(\left( { - 2;\frac{5}{2}} \right)\) thì đồ thị hàm số nằm phía dưới trục hoành. Do đó f(x) < 0 khi x ∈ \(\left( { - 2;\frac{5}{2}} \right)\).
Đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ x = - 2 và x = \(\frac{5}{2}\).
Vậy bất phương trình có tập nghiệm là S = \(\left[ { - 2;\frac{5}{2}} \right]\).
b) Quan sát hình vẽ ta thấy:
Đồ thị hàm số nằm hoàn toàn phía dưới trục hoành với mọi giá trị của x. Do đó f(x) < 0 với mọi x.
Vậy bất phương trình đã cho vô nghiệm.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Toán 10 Bài tập cuối chương 7 có đáp án !!
Copyright © 2021 HOCTAP247
