Từ 6 thẻ số như Hình 2, có thể ghép để tạo thành bao nhiêu

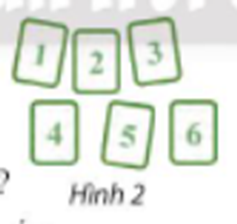
a) Số tự nhiên có sáu chữ số với 6 chữ số được lấy từ 6 thẻ là hoán vị của 6 chữ số. Do đó số số tự nhiên có sáu chữ số là:

P₆ = 6! = 6.5.4.3.2.1 = 720 số.

Vậy có tất cả 720 số tự nhiên có sáu chữ số lấy từ các tấm thẻ.

b) Việc lập số tự nhiên lẻ có sáu chữ số lấy từ 6 thẻ được chia làm hai giai đoạn:

- Giai đoạn 1. Chọn chữ số hàng đơn vị lấy từ các tấm thẻ có chữ số lẻ {1; 3; 5}, có 3 cách.

- Giai đoạn 2. Chọn 5 chữ số còn lại lấy từ 5 tấm thẻ còn lại là hoán vị của 5 chữ số, do đó có 5! = 120 cách.

Theo quy tắc nhân, ta có: 3.120 = 360 số tự nhiên lẻ có sáu chữ số.

Vậy có 360 số tự nhiên lẻ có sáu chữ số.

c) Số số tự nhiên có năm chữ số được lấy từ 6 tấm thẻ là chỉnh hợp chập 5 của 6, do đó có \(A_6^5 = 720\) số.

Vậy có 720 số tự nhiên có 5 chữ số được lấy từ 6 tấm thẻ.

d) Gọi số tự nhiên có năm chữ số cần tìm là \(\overline {abcde} \) (trong đó a, b, c, d, e là các số trên tấm thẻ, a ≠ 0).

Vì \(\overline {abcde} > 50000\) nên a có thể bằng 5 hoặc 6, nghĩa là a có 2 cách chọn.

Bốn chữ số còn lại được chọn từ số trên bốn tấm thẻ còn lại là hoán vị của 4 chữ số, do đó có 4! = 24 cách.

Theo quy tắc nhân, ta có: 2.24 = 48 số tự nhiên có năm chữ số lớn hơn 50 000.