Cho 9 điểm nằm trên hai đường thẳng song song như Hình 3. Có bao nhiêu tam giác có
Câu hỏi :
Cho 9 điểm nằm trên hai đường thẳng song song như Hình 3. Có bao nhiêu tam giác có các đỉnh là ba điểm trong các điểm đã cho?
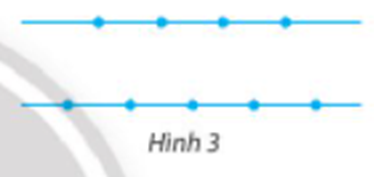
Cho 9 điểm nằm trên hai đường thẳng song song như Hình 3. Có bao nhiêu tam giác có các đỉnh là ba điểm trong các điểm đã cho?

* Đáp án
* Hướng dẫn giải
Đặt tên hai đường thẳng song song lần lượt là d, d’ như hình vẽ:
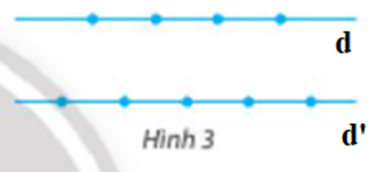
Cách 1: Tam giác có ba đỉnh là ba điểm trong chín điểm đã cho sao cho ba điểm đó không thẳng hàng. Do đó có hai phương án sau:
- Phương án 1: 2 điểm lấy ở đường thẳng d, 1 điểm ở đường thẳng d’, có \(C_4^2.C_5^1 = 30\) cách.
- Phương án 2: 2 điểm lấy ở đường thẳng d’, 1 điểm ở đường thẳng d, có \(C_4^1.C_5^2 = 40\)cách.
Theo quy tắc cộng ta có 30 + 40 = 70 (cách).
Vậy có tất cả 70 tam giác thỏa mãn điều kiện đầu bài.
Cách 2: Tam giác có ba đỉnh là ba điểm trong chín điểm đã cho. Ba điểm được lấy ra phải thỏa mãn ba điểm không cùng nằm trên một đường thẳng. Do đó số tam giác được tạo thành là:
\(C_9^3 - C_4^3 - C_5^3 = 70\)(tam giác).
Vậy có tất cả 70 tam giác thỏa mãn điều kiện đầu bài.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Toán 10 Bài tập cuối chương 8 có đáp án !!
Copyright © 2021 HOCTAP247
