Ta đã biết 1 inch (kí hiệu là in) là 2,54 cm. Màn hình của một chiếc ti vi có dạng hình chữ nhật với độ dài đường chéo là 32 in, tỉ số giữa chiều dài và chiều rộng của màn hình là...

Hướng dẫn giải

Ta mô phỏng màn hình ti vi có hình chữ nhật ABCD như sau:

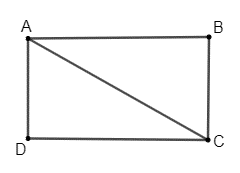
Ta có: AC = 32 in, AB là chiều dài, BC là chiều rộng với AB : BC = 16 : 9.

Gọi chiều dài của ti vi là x (in, x > 0) hay AB = x, khi đó chiều rộng của ti vi là \(BC = \frac{9}{{16}}x\).

Sử dụng định lí Pythagore, ta có phương trình: \({x^2} + {\left( {\frac{9}{{16}}x} \right)^2} = {32^2}\) (*).

Giải phương trình (*), ta có:

(*) \( \Leftrightarrow {x^2} + \frac{{81}}{{256}}{x^2} = 1024\)\( \Leftrightarrow \frac{{337}}{{256}}{x^2} = 1024 \Leftrightarrow {x^2} = \frac{{262144}}{{337}}\)

Do x > 0 nên x = \(\frac{{512}}{{\sqrt {337} }}\).

Vậy chiều dài của chiếc ti vi là \(\frac{{512}}{{\sqrt {337} }} = 27,89041719...\) (in).

Quy tròn số \(\frac{{512}}{{\sqrt {337} }}\) đến hàng phần trăm được 27,89.

Ta có độ chính xác d = 0,005 (nửa đơn vị hàng quy tròn).

Vậy sai số tương đối \({\delta _a} \le \frac{{0,005}}{{27,89}} \approx 0,02\% \).