Giá trị nhỏ nhất Fmin của biểu thức F= –x + y trên miền xác định bởi hệ ( left { { begin{array}{*{20}{c}}{ - 2x + y ge 2} {y - x le 4} {x + 2y ge 5} end{array}} right. ) là:

* Hướng dẫn giải

Đáp án đúng là: A \(\left\{ {\begin{array}{*{20}{c}}{ - 2x + y \ge 2}\\{y - x \le 4}\\{x + 2y \ge 5}\end{array}} \right.\)

Ta biểu diễn miền nghiệm của hệ đã cho trên mặt phẳng tọa độ, ta được hình ảnh sau:

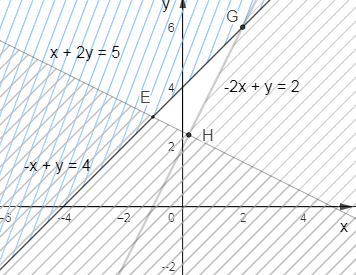
Khi đó miền tam giác EGH (bao gồm cả biên) là miền nghiệm của hệ bất phương trình đã cho.

Các đỉnh E, H, G có tọa độ: E(–1; 3); H(\(\frac{1}{5}\); \(\frac{{12}}{5}\)); G(2; 6).

Ta tính giá trị của F = –x + y tại các đỉnh của tam giác EGH.

Tại E(–1; 3) ta có F = –(–1) + 3 = 4;

Tại H(\(\frac{1}{5}\); \(\frac{{12}}{5}\)) ta có F = – \(\frac{1}{5}\)+\(\frac{{12}}{5}\)= \(\frac{{11}}{5}\);

Tại G(2; 6) ta có F = –2 + 6 = 4.

Suy ra F nhỏ nhất bằng \(\frac{{11}}{5}\) tại H(\(\frac{1}{5}\); \(\frac{{12}}{5}\)), tức là F_min = \(\frac{{11}}{5}\).

Ta chọn đáp án A.