Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa
Câu hỏi :
Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (một sản phẩm mới của công ty) cần thuê xe để chở trên 140 người và trên 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó loại xe A có 10 chiếc, loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng.
Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (một sản phẩm mới của công ty) cần thuê xe để chở trên 140 người và trên 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó loại xe A có 10 chiếc, loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng.
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
Đáp án đúng là: B
Gọi x là số xe loại A được thuê, y là số xe loại B được thuê. (x ≥ 0, y ≥ 0)
Do loại xe A có 10 chiếc, loại xe B có 9 chiếc nên x ≤ 10, y ≤ 9.
Do xe A chỉ chở tối đa 20 người và 0,6 tấn hàng, xe B chở tối đa 10 người và 1,5 tấn hàng mà cần thuê xe để chở trên 140 người và trên 9 tấn hàng nên:
Khi đó ta có hệ bất phương trình của x và y như sau:
⇔
Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy:
- Biểu diễn miền nghiệm D1 của bất phương trình x ≥ 0.
+ Đường thẳng x = 0 là trục Oy.
Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy (kể cả bờ Oy) nằm bên phải trục Oy.
* Tương tự ta biểu diễn các miền nghiệm:
- Miền nghiệm D2 của bất phương trình y ≥ 0: là nửa mặt phẳng bờ Ox (kể cả bờ Ox) nẳm bên trên trục Ox.
- Miền nghiệm D3 của bất phương trình x ≤ 10: là nửa mặt phẳng bờ d1 (kể cả bờ d1: x = 10) chứa điểm O.
- Miền nghiệm D4 của bất phương trình y ≤ 9: là nửa mặt phẳng bờ d2 (kể cả bờ d2: y = 9) chứa điểm O.
- Miền nghiệm D5 của bất phương trình 2x + y ≥ 14:
+ Vẽ đường thẳng d3: 2x + y = 14.
+ Xét điểm O(0; 0): thay x = 0, y = 0 vào bất phương trình ta có 2. 0 + 0 = 0 ≥ 14 là mệnh đề sai nên điểm O(0; 0) không thỏa mãn bất phương trình 2x + y ≥ 14.
Miền nghiệm D5 của bất phương trình 2x + y ≥ 14 là nửa mặt phẳng bờ d3 (kể cả bờ d3) không chứa điểm O.
- Tương tự miền nghiệm D6 của bất phương trình 2x + 5y ≥ 30 là nửa mặt phẳng bờ d4 (kể cả bờ d4: 2x + 5y = 30) không chứa điểm O.
Ta có đồ thị:
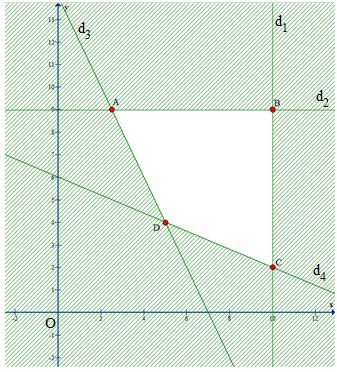
Miền nghiệm của hệ bất phương trình là miền tứ giác ABCD:
A(2,5; 9), B(10; 9), C(10; 2), D(5; 4)
Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu nên tổng số tiền thuê là:
F (x; y) = 4x + 3y.
Để chi phí vận chuyển là thấp nhất thì F (x; y) là nhỏ nhất.
Tại A(2,5; 9): F = 4. 2,5 + 3. 9 = 37;
Tại B(10; 9): F = 4. 10 + 3. 9 = 67;
Tại C(10; 2): F = 4. 10 + 3. 2 = 46;
Tại D(5; 4): F = 4. 5 + 3. 4 = 32;
Vậy F (x; y) đạt giá trị nhỏ nhất là 32 khi x = 5 và y = 4.
Vậy cần thuê 5 xe loại A và 4 xe loại B để số tiền thuê nhỏ nhất.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 Ôn tập chương 2 có đáp án !!
Copyright © 2021 HOCTAP247
