Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và

* Hướng dẫn giải

Hướng dẫn giải

Đáp án đúng là: C

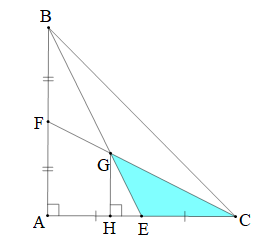
Vì BE là trung tuyến của tam giác ABC nên E là trung điểm của AC.

Do đó $EC=\frac{1}{2}.AC=\frac{1}{2}.30=15\left(cm\right)$ 

Hai đường trung tuyến BE và CF cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Khi đó $GE=\frac{1}{3}BE$ (tính chất trọng tâm của tam giác)

Hay $\frac{GE}{BE}=\frac{1}{3}.$ 

Gọi H là chân đường vuông góc kẻ từ G xuống AC.

Suy ra GH // AB.

Do đó $\frac{GH}{BA}=\frac{GE}{BE}$ (định lí Ta – let trong tam giác ABE)

Hay $\frac{GH}{BA}=\frac{1}{3}\Rightarrow GH=\frac{1}{3}.BA=\frac{1}{3}.30=10\left(cm\right)$

Diện tích tam giác GEC là: $S_{GEC}=\frac{1}{2}.GH.EC=\frac{1}{2}\mathrm{.10.15}=75\left(c{m}^2\right)$ 

Vậy diện tích tam giác GEC là 75 cm².