Cho ba vectơ a, vecto b, vecto c cùng phương và cùng khác vectơ 0. Chứng minh rằng có ít nhất hai vectơ trong chúng có cùng hướng

* Hướng dẫn giải

Lời giải

Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) cùng phương và cùng khác vectơ \(\overrightarrow 0 \) nên chúng có thể cùng hướng hoặc ngược hướng nhau.

Trường hợp 1: Nếu \[\overrightarrow a \] cùng hướng với \(\overrightarrow b \) (hoặc \(\overrightarrow a \) cùng hướng với \(\overrightarrow c \))

Thì khi đó có hai vectơ cùng hướng.

Trường hợp 2: Nếu \[\overrightarrow a \] ngược hướng với cả \(\overrightarrow b \) và \(\overrightarrow c \)

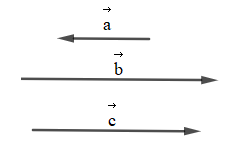
Vì \[\overrightarrow a \] ngược hướng với \(\overrightarrow b \), \[\overrightarrow a \] ngược hướng với \(\overrightarrow c \)

Nên khi đó \(\overrightarrow b \) và \(\overrightarrow c \) cùng hướng với nhau.

Do đó có hai vectơ trong ba vectơ cùng hướng với nhau

Vậy có ít nhất hai vectơ trong ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) có cùng hướng.