Cho lục giác đều ABCDEF có tâm O. Xét các vectơ có hai điểm mút lấy từ các điểm O, A, B, C, D, E, F.a) Hãy chỉ ra các vectơ khác vectơ - không và cùng phương với vectơ OA

* Hướng dẫn giải

Lời giải

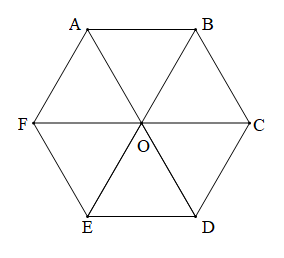
Do ABCDEF là lục giác đều tâm O nên:

+ Các cặp cạnh đối diện bằng nhau: AB = ED, BC = FE, CD = FA;

+ Ba đường chéo chính AD, BE, CF đồng quy tại trung điểm của mỗi đường;

+ Mỗi đường chéo chính song song với một cặp cạnh có đầu mút không thuộc đường chéo ấy.

a) Các vectơ khác vectơ - không và cùng phương với vectơ \(\overrightarrow {OA} \) mà có hai điểm mút lấy từ các điểm O, A, B, C, D, E, F là: \(\overrightarrow {OA} ,\overrightarrow {AO} ,\overrightarrow {OD} ,\overrightarrow {DO} ,\overrightarrow {BC} ,\overrightarrow {CB} ,\overrightarrow {EF} ,\overrightarrow {FE} ,\overrightarrow {DA} ,\overrightarrow {AD} .\)

b) Vectơ bằng vectơ \(\overrightarrow {AB} \) mà có hai điểm mút lấy từ các điểm O, A, B, C, D, E, F là: \(\overrightarrow {AB} ,\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} .\)