Cho tam giác ABC không vuông, với trực tâm H, nội tiếp đường tròn (O). Kẻ đường kính AA' của đường tròn (O).Gọi M là trung điểm cạnh BC. Tìm mối quan hệ về phương, hướng và độ dài...

* Hướng dẫn giải

Lời giải

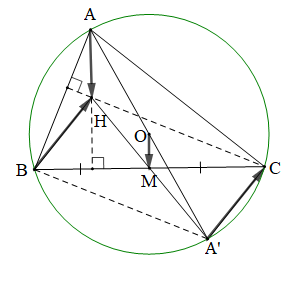
Ta có: O và M lần lượt là trung điểm của AA' và BC

Nên OM là đường trung bình của tam giác AA'H

Do đó AH = 2OM và OM // AH (tính chất đường trung bình)

Vậy, hai vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {AH} \) có:

+ Cùng phương

+ Cùng hướng

+ \(\left| {\overrightarrow {AH} } \right| = 2\left| {\overrightarrow {OM} } \right|\)