Cho hai vectơ a và vecto b không cùng phương. Chứng minh rằng:| vecto a | - | vecto b |

* Hướng dẫn giải

Lời giải

Giả sử ba điểm A, B, C thoả mãn: \(\overrightarrow a = \overrightarrow {AB} ,\overrightarrow b = \overrightarrow {BC} \)

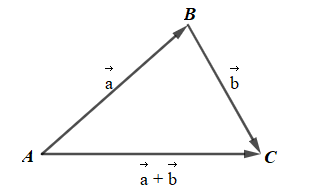
Khi đó ta có: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (quy tắc ba điểm)

Do đó:

+) \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow {AB} } \right| = AB;\)

+) \(\left| {\overrightarrow b } \right| = \left| {\overrightarrow {BC} } \right| = BC;\)

+) \(\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow {AC} } \right| = AC\)

Mặt khác: xét tam giác ABC, theo bất đẳng thức trong tam giác ta có:

AB – BC < AC < AB + BC

Hay \[\left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| < \left| {\overrightarrow a + \overrightarrow b } \right| < \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\] \(\)

Vậy \(\left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| < \left| {\overrightarrow a + \overrightarrow b } \right| < \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|.\)