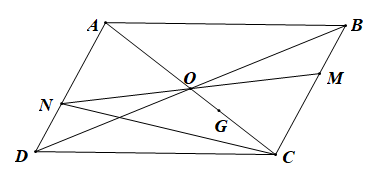
Cho hình bình hành ABCD tâm O. M là một điểm tuỳ ý thuộc cạnh BC, khác B và C. MO cắt cạnh AD tại N. Chứng minh rằng O là trung điểm MN.

* Hướng dẫn giải

Lời giải

Vì

ABCD là hình bình hành tâm O

Nên O là trung điểm của AC và BD và \(\widehat {ADO} = \widehat {CBO}\)

Xét ∆ODN và ∆OBM có:

OD = OB (do O là trung điểm của BD),

\(\widehat {DON} = \widehat {BOM}\) (hai góc đối đỉnh),

\(\widehat {NDO} = \widehat {MBO}\)(do \(\widehat {ADO} = \widehat {CBO}\))

∆ODN = ∆OBM (g.c.g)

ON = OM (hai cạnh tương ứng)

O là trung điểm của NM.

Vậy O là trung điểm của NM.