Cho hình bình hành ABCD tâm O. M là một điểm tuỳ ý thuộc cạnh BC, khác B và C. MO cắt cạnh AD tại N. Gọi G là trọng tâm tam giác BCD. Chứng minh rằng G cũng là trọng tâm tam giác M...

* Hướng dẫn giải

Lời giải

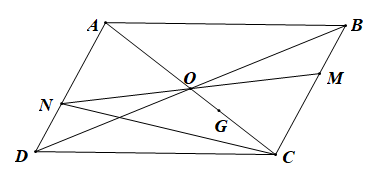
Vì

G là trọng tâm ∆BCD nên \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)

\( \Rightarrow \left( {\overrightarrow {GM} + \overrightarrow {MB} } \right) + \overrightarrow {GC} + \left( {\overrightarrow {GN} + \overrightarrow {ND} } \right) = \overrightarrow 0 \) (quy tắc hiệu)

\( \Rightarrow \overrightarrow {GM} + \overrightarrow {MB} + \overrightarrow {GC} + \overrightarrow {GN} + \overrightarrow {ND} = \overrightarrow 0 \)

\[ \Rightarrow \overrightarrow {GM} + \overrightarrow {GC} + \overrightarrow {GN} + \left( {\overrightarrow {MB} + \overrightarrow {ND} } \right) = \overrightarrow 0 \] (*)

Ta có: O là trung điểm của NM (câu a), O là trung điểm của BD (câu a)

BMDN là hình bình hành

\( \Rightarrow \overrightarrow {BM} = \overrightarrow {ND} \) \( \Rightarrow - \overrightarrow {MB} = \overrightarrow {ND} \)

\( \Rightarrow \overrightarrow {MB} + \overrightarrow {ND} = \overrightarrow 0 \)

Thay vào (*) ta được \[\overrightarrow {GM} + \overrightarrow {GC} + \overrightarrow {GN} + \overrightarrow 0 = \overrightarrow 0 \]

Do đó \[\overrightarrow {GM} + \overrightarrow {GC} + \overrightarrow {GN} = \overrightarrow 0 \]

G là trọng tâm tam giác MNC.

Vậy G là trọng tâm tam giác MNC.