Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của các cạnh BC, CA. AB.Xác định vectơ AF - vectơ BD + vectơ CE

* Hướng dẫn giải

Lời giải

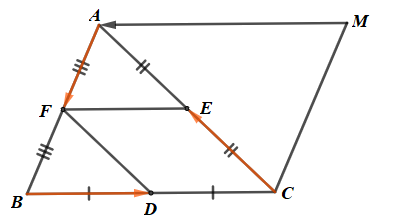
Ta có: \[\overrightarrow {AF} --\overrightarrow {BD} + \overrightarrow {CE} \]

\( = \overrightarrow {AF} + \overrightarrow {DB} + \overrightarrow {CE} \)

\( = \overrightarrow {AF} + \overrightarrow {DB} + \overrightarrow {EA} \) (vì E là trung điểm AC nên \(\overrightarrow {CE} = \overrightarrow {EA} \))

\( = \left( {\overrightarrow {EA} + \overrightarrow {AF} } \right) + \overrightarrow {DB} \)

\( = \overrightarrow {EF} + \overrightarrow {DB} \)

Vì E, F lần lượt là trung điểm của AC, AB

Nên EF là đường trung bình của tam giác ABC

EF // BC và \(EF = \frac{1}{2}BC\)

Mà D là trung điểm của BC nên \(BD = \frac{1}{2}BC\)

Xét tứ giác EFBD có: EF // BD, \[{\rm{EF}} = BD\left( { = \frac{1}{2}BC} \right)\]

EFBD là hình bình hành

\(\overrightarrow {EF} = \overrightarrow {DB} \)

Khi đó: \[\overrightarrow {AF} --\overrightarrow {BD} + \overrightarrow {CE} \]\( = \overrightarrow {EF} + \overrightarrow {DB} \)

\( = \overrightarrow {DB} + \overrightarrow {DB} \)

\( = 2\overrightarrow {DB} \)

\( = \overrightarrow {CB} \) (do D là trung điểm của BC)

Vậy \[\overrightarrow {AF} --\overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {CB} .\]