Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của các cạnh BC, CA. AB. Xác định điểm M thoả mãn vecto AF - vecto BD + vecto CE

* Hướng dẫn giải

Lời giải

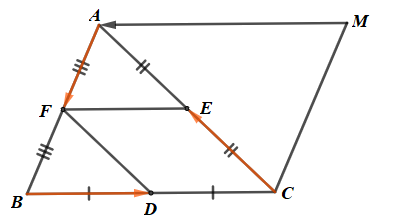
Điểm M thoả mãn \[\overrightarrow {{\rm{AF}}} - \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {MA} .\]

Mà \[\overrightarrow {AF} --\overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {CB} \] (câu a)

Nên \(\overrightarrow {MA} = \overrightarrow {CB} \)

Do đó MABC là hình bình hành (theo kết quả bài tập 4.3 SGK Toán 10 tập 1)

Vậy điểm M thoả mãn tứ giác MABC là hình bình hành.