Trên mặt phẳng, chất điểm A chịu tác dụng của ba lực vecto F1 , vecto F2 , vecto F3và ở trạng thái cân bằng. Góc giữa hai vectơ

* Hướng dẫn giải

Lời giải

Ta sử dụng các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) và \(\overrightarrow {AE} \) lần lượt biểu diễn cho các lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) và hợp lực \(\overrightarrow F \) của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) (hình vẽ dưới đây).

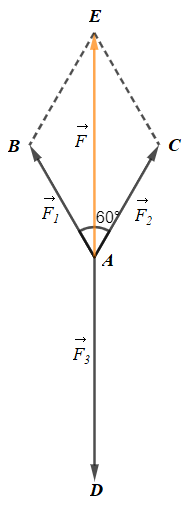
Khi đó do \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) nên tứ giác ABEC là hình bình hành

Lại có góc giữa hai vectơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) bằng 60° nên \(\widehat {BAC} = 60^\circ \)

Suy ra \(\widehat {ECA} = 180^\circ - \widehat {BAC} = 180^\circ - 60^\circ = 120^\circ \)

Áp dụng định lí Cosin cho tam giác AEC ta có:

AE² = AC² + EC² – 2.AC.EC.cos\(\widehat {ECA}\)

Hay \(A{E^2} = {\left( {2\sqrt 3 } \right)^2} + {\left( {2\sqrt 3 } \right)^2} - 2.2\sqrt 3 .2\sqrt 3 .c{\rm{os120}}^\circ \)

AE² = 36

AE = 6

Do đó \(\left| {\overrightarrow F } \right| = 6\,\left( N \right)\)

Vì chất điểm A ở trạng thái cân bằng nên hai lực \(\overrightarrow F \) và \(\overrightarrow {{F_3}} \) ngược hướng và có cường độ bằng nhau

Tức là hai vectơ \(\overrightarrow {AE} \) và \(\overrightarrow {AD} \) là hai vectơ đối nhau

Do đó độ lớn của lực \(\overrightarrow {{F_3}} \) bằng \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow F } \right| = 6\,\left( N \right)\)

Vậy độ lớn của lực \(\overrightarrow {{F_3}} \) bằng 6 N.