Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S theo thứ tự là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

* Hướng dẫn giải

Lời giải

+)

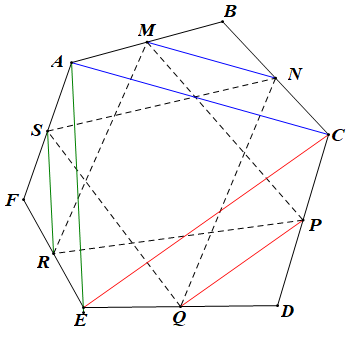
Vì M, N lần lượt là trung điểm của AB, BC

Nên MN là đường trung bình của tam giác ABC.

MN // AC và \(MN = \frac{1}{2}AC\) (tính chất đường trung bình)

Do đó \(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} \)(1)

Chứng minh tương tự ta cũng có: \(\overrightarrow {PQ} = \frac{1}{2}\overrightarrow {CE} \)(2)

Và \(\overrightarrow {RS} = \frac{1}{2}\overrightarrow {EA} \)(3)

Từ (1), (2) và (3) ta có:

\(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \frac{1}{2}\overrightarrow {AC} + \frac{1}{2}\overrightarrow {CE} + \frac{1}{2}\overrightarrow {EA} \)

\( = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right)\)

\( = \frac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {EA} } \right)\) (quy tắc ba điểm)

\( = \frac{1}{2}\overrightarrow {{\rm{AA}}} \)(quy tắc ba điểm)

\( = \frac{1}{2}.\overrightarrow 0 = \overrightarrow 0 \)

Do đó \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0 \)

+) Giả sử G và G' lần lượt là trọng tâm của tam giác MPR và tam giác NQS.

Khi đó ta có: \(\overrightarrow {MG} + \overrightarrow {PG} + \overrightarrow {RG} = \overrightarrow 0 \) và \(\overrightarrow {NG'} + \overrightarrow {QG'} + \overrightarrow {SG'} = \overrightarrow 0 \) hay \(\overrightarrow {G'N} + \overrightarrow {G'Q} + \overrightarrow {G'S} = \overrightarrow 0 \)

Mặt khác: theo quy tắc ba điểm ta có:

+) \(\overrightarrow {MN} = \overrightarrow {MG} + \overrightarrow {GG'} + \overrightarrow {G'N} ;\)

+) \(\overrightarrow {PQ} = \overrightarrow {PG} + \overrightarrow {GG'} + \overrightarrow {G'Q} ;\)

+) \(\overrightarrow {RS} = \overrightarrow {RG} + \overrightarrow {GG'} + \overrightarrow {G'S} ;\)

\( \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow {MG} + \overrightarrow {PG} + \overrightarrow {RG} + 3.\overrightarrow {GG'} + \overrightarrow {G'N} + \overrightarrow {G'Q} + \overrightarrow {G'S} \)

\( = \left( {\overrightarrow {MG} + \overrightarrow {PG} + \overrightarrow {RG} } \right) + 3.\overrightarrow {GG'} + \left( {\overrightarrow {G'N} + \overrightarrow {G'Q} + \overrightarrow {G'S} } \right)\)

\( = \overrightarrow 0 + 3.\overrightarrow {GG'} + \overrightarrow 0 \)

\( = 3.\overrightarrow {GG'} \)

+) Lại có \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0 \) (chứng minh trên)

Nên \(3\overrightarrow {GG'} = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {GG'} = \overrightarrow 0 \)

Suy ra G và G' trùng nhau.

Vậy hai tam giác MPR và NQS có cùng trọng tâm.