Cho tam giác ABC.Xác định điểm N thoả mãn 4 vecto NA - 2 vecto NB + vecto NC = vecto 0

* Hướng dẫn giải

Lời giải

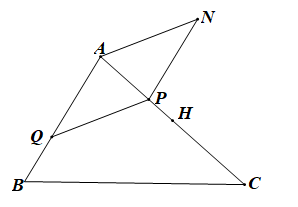
Ta có: \[4\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} = 4\overrightarrow {NA} - 2\left( {\overrightarrow {NA} + \overrightarrow {AB} } \right) + \overrightarrow {NC} \]

\[ = 4\overrightarrow {NA} - 2\overrightarrow {NA} - 2\overrightarrow {AB} + \overrightarrow {NC} \]

\[ = 2\overrightarrow {NA} - 2\overrightarrow {AB} + \overrightarrow {NC} \]

\[ = \overrightarrow {NA} - 2\overrightarrow {AB} + \left( {\overrightarrow {NA} + \overrightarrow {NC} } \right)\]

Gọi H là trung điểm của AC, khi đó \(\overrightarrow {NA} + \overrightarrow {NC} = 2\overrightarrow {NH} \)

\[ \Rightarrow 4\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow {NA} - 2\overrightarrow {AB} + 2.\overrightarrow {NH} \]

\[ = \left( {\overrightarrow {NA} + 2.\overrightarrow {NH} } \right) - 2\overrightarrow {AB} \]

Giả sử P là điểm thỏa mãn \[\overrightarrow {PA} + 2.\overrightarrow {PH} = \overrightarrow 0 \]

Khi đó \[\overrightarrow {NA} + 2.\overrightarrow {NH} = \left( {\overrightarrow {NP} + \overrightarrow {PA} } \right) + 2\left( {\overrightarrow {NP} + \overrightarrow {PH} } \right)\]

\( = 3\overrightarrow {NP} + \overrightarrow {PA} + 2\overrightarrow {PH} \)

\( = 3\overrightarrow {NP} + \overrightarrow 0 \)

\( = 3\overrightarrow {NP} \)

\( \Rightarrow 4\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} = 3\overrightarrow {NP} - 2\overrightarrow {AB} \)

Mà \[4\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 .\]

Nên \(3\overrightarrow {NP} - 2\overrightarrow {AB} = \overrightarrow 0 \)

\( \Rightarrow 3\overrightarrow {NP} = 2\overrightarrow {AB} \)

\[ \Rightarrow \overrightarrow {NP} = \frac{2}{3}\overrightarrow {AB} \]

Gọi Q là điểm nằm trên cạnh AB sao cho \[\overrightarrow {AQ} = \frac{2}{3}\overrightarrow {AB} \]

\[ \Rightarrow \overrightarrow {NP} = \overrightarrow {AQ} \]

Do đó tứ giác AQPN là hình bình hành

Vậy điểm N cần tìm là đỉnh của hình bình hành AQPN (với Q thỏa mãn \[\overrightarrow {AQ} = \frac{2}{3}\overrightarrow {AB} \] và P thỏa mãn \[\overrightarrow {PA} + 2.\overrightarrow {PH} = \overrightarrow 0 \], H là trung điểm của AC).