Cho tam giác ABC.Tìm tập hợp các điểm M thoả mãn | vecto MA + vecto 2MB + 3 vecto MC| = | vecto MB

* Hướng dẫn giải

Lời giải

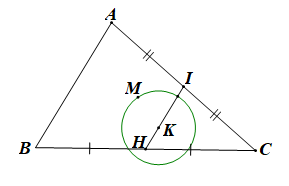
Chứng minh tương tự câu a ta có:

\(\overrightarrow {MA} + \overrightarrow {2MB} + 3\overrightarrow {MC} = 2\overrightarrow {MI} + 4\overrightarrow {MH} \)

\( = 2\left( {\overrightarrow {MK} + \overrightarrow {KI} } \right) + 4\left( {\overrightarrow {MK} + \overrightarrow {KH} } \right)\)

\( = 2\overrightarrow {MK} + 2\overrightarrow {KI} + 4\overrightarrow {MK} + 4\overrightarrow {KH} \)

\( = 6\overrightarrow {MK} + \left( {2\overrightarrow {KI} + 4\overrightarrow {KH} } \right)\)

Mà \[2\overrightarrow {KI} + 4\overrightarrow {KH} = \overrightarrow 0 \] (câu a)

Nên \(\overrightarrow {MA} + \overrightarrow {2MB} + 3\overrightarrow {MC} = 6\overrightarrow {MK} \)

Lại có: \(\overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow {CB} \)

Do đó \(\left| {\overrightarrow {MA} + \overrightarrow {2MB} + 3\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB} - \overrightarrow {MC} } \right|.\)

\( \Leftrightarrow \left| {6\overrightarrow {MK} } \right| = \left| {\overrightarrow {CB} } \right|\)

6MK = CB

\( \Leftrightarrow KM = \frac{{BC}}{6}\)

Do đó tập hợp điểm M là đường tròn tâm K, bán kính bằng \(\frac{{BC}}{6}\) như hình vẽ.