Để kéo đường dây điện băng qua một hồ hình chữ nhật ABCD với độ dài AB = 200 m, AD = 180 m, người ta dự định làm 4 cột điện liên tiếp cách đều, cột thứ nhất nằm trên bờ AB và cách...

* Hướng dẫn giải

Lời giải

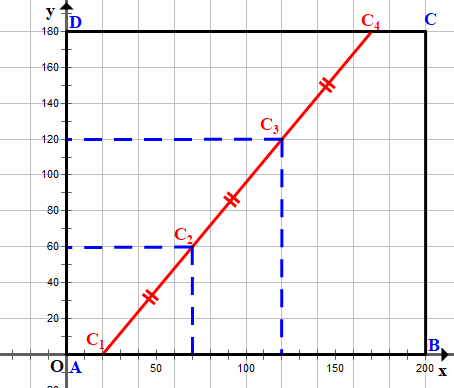
Chọn hệ trục tọa độ Oxy sao cho các đỉnh của hình hồ hình chữ nhật có các tọa độ là A(0; 0), B(200; 0), C(200; 180) và D(0; 180).

Gọi vị trí các cột điện được trồng là C₁, C₂, C₃ và C₄.

Vì vị trí cột điện thứ nhất C₁ nằm trên bờ AB và cách A một khoảng 20 m nên trong hệ trục tọa độ đã chọn, điểm C₁(20; 0).

Vị trí cột điện thứ tư nằm trên bờ CD và cách C một khoảng 30 m nên khoảng cách từ C₄ đến D là 170 m. Khi đó trong hệ trục tọa độ đã chọn, điểm C₄(170; 180).

Vì bốn cột điện được trồng liên tiếp nhau và cách đều trên một đường thẳng nên:

C₁C₂ = C₂C₃ = C₃C₄

C₁C₂ = \(\frac{1}{3}\)C₁C₄ và C₁C₃ = \(\frac{2}{3}\)C₁C₄.

\( \Rightarrow \overrightarrow {{C_1}{C_2}} = \frac{1}{3}\overrightarrow {{C_1}{C_4}} \) và \(\overrightarrow {{C_1}{C_3}} = \frac{2}{3}\overrightarrow {{C_1}{C_4}} \)

Giả sử C₂(a; b) và C₃(x; y).

Với C₁(20; 0), C₄(170; 180) ta có:

\(\overrightarrow {{C_1}{C_4}} = \left( {150;180} \right)\); \(\overrightarrow {{C_1}{C_2}} = \left( {a - 20;b} \right)\) và \(\overrightarrow {{C_1}{C_3}} = \left( {x - 20;y} \right)\)

• \[\overrightarrow {{C_1}{C_2}} = \frac{1}{3}\overrightarrow {{C_1}{C_4}} \Leftrightarrow \left\{ \begin{array}{l}a - 20 = \frac{1}{3}.150 = 50\\b = \frac{1}{3}.180 = 60\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}a = 70\\b = 60\end{array} \right.\] C₂(70; 60).

d(C₂; AB) = d(C₂; Ox) = |b| = 60 (m).

d(C₂; AD) = d(C₂; Oy) = |a| = 70 (m).

• \(\overrightarrow {{C_1}{C_3}} = \frac{2}{3}\overrightarrow {{C_1}{C_4}} \)\[ \Leftrightarrow \left\{ \begin{array}{l}x - 20 = \frac{2}{3}.150 = 100\\y = \frac{2}{3}.180 = 120\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}x = 120\\y = 120\end{array} \right.\] C₃(120; 120).

d(C₃; AB) = d(C₃; Ox) = |y| = 120 (m)

d(C₃; AD) = d(C₃; Oy) = |x| = 120 (m).

Vậy khoảng cách từ cột điện thứ hai đến bờ AB là 60 m và đến bờ AD là 70 m.

Khoảng cách từ cột điện thứ ba đến bờ AB là 120 m và đến bờ AD là 120 m.