Cho tam giác đều ABC có độ dài các cạnh bằng 1. Gọi M là trung điểm của BC. Tính tích vô hướng của các cặp vectơ vecto MA và vecto BA, vectoMA
Câu hỏi :
Cho tam giác đều ABC có độ dài các cạnh bằng 1.
* Đáp án
* Hướng dẫn giải
Lời giải
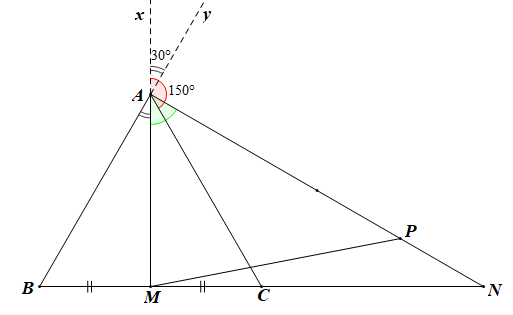
Tam giác ABC đều có M là trung điểm của BC nên đường trung tuyến AM đồng thời là đường phân giác và đường cao.
\( \Rightarrow \widehat {BAM} = \widehat {MAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.60^\circ = 30^\circ \)
Gọi Ax là tia đối của tia AM, tia Ay là tia đối của tia AB.
Do đó \(\left( {\overrightarrow {MA} ;\overrightarrow {BA} } \right) = \widehat {xAy} = \widehat {BAM} = 30^\circ \)
\(\left( {\overrightarrow {MA} ;\overrightarrow {AC} } \right) = \widehat {xAC} = 180^\circ - \widehat {MAC}\)
\( \Rightarrow \left( {\overrightarrow {MA} ;\overrightarrow {AC} } \right) = 180^\circ - 30^\circ = 150^\circ \)
Khi đó ta có:
• \(\overrightarrow {MA} .\overrightarrow {BA} = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {BA} } \right|.c{\rm{os}}\left( {\overrightarrow {MA} ;\overrightarrow {BA} } \right)\)
\( \Rightarrow \overrightarrow {MA} .\overrightarrow {BA} = MA.BA.c{\rm{os30}}^\circ \)
Xét tam giác BAM vuông tại M, theo định lí Pythagoras ta có:
\(MA = \sqrt {B{A^2} - B{M^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
\( \Rightarrow \overrightarrow {MA} .\overrightarrow {BA} = \frac{{\sqrt 3 }}{2}.1.\frac{{\sqrt 3 }}{2} = \frac{3}{4}.\)
• \(\overrightarrow {MA} .\overrightarrow {AC} = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {AC} } \right|.c{\rm{os}}\left( {\overrightarrow {MA} ;\overrightarrow {AC} } \right)\)
\( \Rightarrow \overrightarrow {MA} .\overrightarrow {AC} = MA.AC.c{\rm{os150}}^\circ \)
\[ \Rightarrow \overrightarrow {MA} .\overrightarrow {AC} = \frac{{\sqrt 3 }}{2}.1.\frac{{ - \sqrt 3 }}{2} = \frac{{ - 3}}{4}.\]
Vậy \(\overrightarrow {MA} .\overrightarrow {BA} = \frac{3}{4}\) và \(\overrightarrow {MA} .\overrightarrow {AC} = \frac{{ - 3}}{4}.\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 Bài 11. Tích vô hướng của hai vectơ có đáp án !!
Copyright © 2021 HOCTAP247
