Cho tam giác đều ABC có độ dài các cạnh bằng 1. Lấy điểm P thuộc đoạn AN sao cho AP = 3PN. Hãy biểu thị các vectơ AP , vecto MP theo hai vectơ

* Hướng dẫn giải

Lời giải

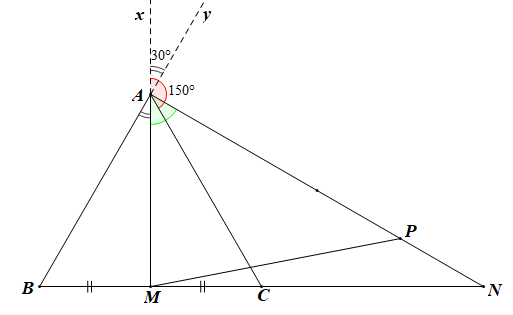
• Vì P thuộc đoạn thẳng AN thỏa mãn AP = 3PN \( \Rightarrow AP = \frac{3}{4}AN\)

\( \Rightarrow \overrightarrow {AP} = \frac{3}{4}\overrightarrow {AN} = \frac{3}{4}.\left( {2\overrightarrow {AC} - \overrightarrow {AB} } \right)\)

\( \Rightarrow \overrightarrow {AP} = \frac{3}{2}\overrightarrow {AC} - \frac{3}{4}\overrightarrow {AB} \)

• Ta có: \(\overrightarrow {MP} = \overrightarrow {AP} - \overrightarrow {AM} \)

\( = \left( {\frac{3}{2}\overrightarrow {AC} - \frac{3}{4}\overrightarrow {AB} } \right) - \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)

\( = \frac{3}{2}\overrightarrow {AC} - \frac{3}{4}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AC} \)

\( = \left( {\frac{3}{2}\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AC} } \right) - \left( {\frac{3}{4}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AB} } \right)\)

\( = \overrightarrow {AC} - \frac{5}{4}\overrightarrow {AB} \)

\( \Rightarrow MP = \left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {AC} - \frac{5}{4}\overrightarrow {AB} } \right|\)

\( \Rightarrow M{P^2} = {\left( {\overrightarrow {AC} - \frac{5}{4}\overrightarrow {AB} } \right)^2}\)

\( = {\overrightarrow {AC} ^2} - 2.\frac{5}{4}\overrightarrow {AC} .\overrightarrow {AB} + \frac{{25}}{{16}}{\overrightarrow {AB} ^2}\)

\( = A{C^2} + \frac{{25}}{{16}}A{B^2} - \frac{5}{2}\overrightarrow {AC} .\overrightarrow {AB} \)

\( = {1^2} + \frac{{25}}{{16}}{.1^2} - \frac{5}{2}.\frac{1}{2}\)

\( = \frac{{21}}{{16}}\)

\( \Rightarrow MP = \sqrt {\frac{{21}}{{16}}} = \frac{{\sqrt {21} }}{4}.\)

Vậy \(\overrightarrow {AP} = \frac{3}{2}\overrightarrow {AC} - \frac{3}{4}\overrightarrow {AB} ;\)\(\overrightarrow {MP} = \overrightarrow {AC} - \frac{5}{4}\overrightarrow {AB} \) và \(MP = \frac{{\sqrt {21} }}{4}.\)