Cho hình chữ nhật ABCD có AB = 1, BC = căn bậc hai 2 Gọi M là trung điểm của AD. Gọi H là giao điểm của AC, BM. Gọi N là trung điểm của AH và P là trung điểm của CD. Chứng minh rằn...
Câu hỏi :
Cho hình chữ nhật ABCD có AB = 1, \(BC = \sqrt 2 .\) Gọi M là trung điểm của AD.
* Đáp án
* Hướng dẫn giải
Lời giải
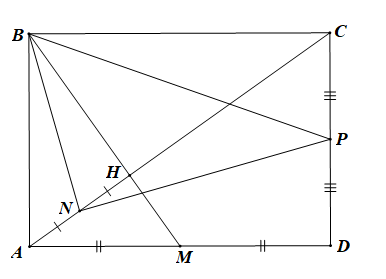
• Xét tam giác ABC vuông tại C, theo định lí Pythagore ta có:
AC2 = AB2 + BC2 = 1 + \({\left( {\sqrt 2 } \right)^2}\)= 3
\( \Rightarrow AC = \sqrt 3 \)
Theo hệ thức lượng trong tam giác vuông ta có:
AB2 = AH.AC \( \Rightarrow AH = \frac{{A{B^2}}}{{AC}} = \frac{{{1^2}}}{{\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
\[ \Rightarrow \frac{{AH}}{{AC}} = \frac{{\sqrt 3 }}{3}:\sqrt 3 = \frac{1}{3}\]
\( \Rightarrow \overrightarrow {AH} = \frac{1}{3}\overrightarrow {AC} \)
Khi đó \(\overrightarrow {HC} = \frac{2}{3}\overrightarrow {AC} \) và \(\overrightarrow {HA} = - \frac{1}{3}\overrightarrow {AC} \)
Ta có \(\overrightarrow {NB} = \overrightarrow {NA} + \overrightarrow {AB} \) (quy tắc ba điiểm)
Vì N là trung điểm của AH nên \(\overrightarrow {NA} = \frac{1}{2}\overrightarrow {HA} \)
\( \Rightarrow \overrightarrow {NB} = \frac{1}{2}.\left( { - \frac{1}{3}\overrightarrow {AC} } \right) + \overrightarrow {AB} \)
\( = - \frac{1}{6}.\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow a \)
\( = \frac{5}{6}\overrightarrow a - \frac{1}{6}\overrightarrow b \)
• Có N là trung điểm của HA và P là trung điểm của CD, theo kết quả bài 4.12, trang 58, Sách giáo khoa Toán 10, tập một, ta có:
\(\overrightarrow {AD} + \overrightarrow {HC} = 2\overrightarrow {NP} \)\( \Rightarrow \overrightarrow {NP} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {HC} } \right)\)
\( \Rightarrow \overrightarrow {NP} = \frac{1}{2}\overrightarrow {AD} + \frac{1}{2}\overrightarrow {HC} \)
\( = \frac{1}{2}\overrightarrow {AD} + \frac{1}{2}.\frac{2}{3}\overrightarrow {AC} \)
\( = \frac{1}{2}\overrightarrow b + \frac{1}{3}.\left( {\overrightarrow a + \overrightarrow b } \right)\)
\( = \frac{1}{3}\overrightarrow a + \frac{5}{6}.\overrightarrow b \)
Khi đó \[\overrightarrow {NB} .\overrightarrow {NP} = \left( {\frac{5}{6}\overrightarrow a - \frac{1}{6}\overrightarrow b } \right).\left( {\frac{1}{3}\overrightarrow a + \frac{5}{6}.\overrightarrow b } \right)\]
\[ = \frac{5}{{18}}{\overrightarrow a ^2} + \frac{{25}}{{36}}\overrightarrow a .\overrightarrow b - \frac{1}{{18}}\overrightarrow a .\overrightarrow b - \frac{5}{{36}}{\overrightarrow b ^2}\]
\[ = \frac{5}{{18}}{\overrightarrow a ^2} + \frac{{25}}{{36}}\overrightarrow a .\overrightarrow b - \frac{1}{{18}}\overrightarrow a .\overrightarrow b - \frac{5}{{36}}{\overrightarrow b ^2}\]
\[ = \frac{5}{{18}}{\left| {\overrightarrow a } \right|^2} + \frac{{25}}{{36}}\overrightarrow 0 - \frac{1}{{18}}\overrightarrow 0 - \frac{5}{{36}}{\left| {\overrightarrow b } \right|^2}\] (do \(\overrightarrow a .\overrightarrow b = \overrightarrow 0 \))
\[ = \frac{5}{{18}}{.1^2} - \frac{5}{{36}}.{\left( {\sqrt 2 } \right)^2}\]
\[ = \frac{5}{{18}} - \frac{5}{{36}}.2 = 0\]
Do đó \[\overrightarrow {NB} .\overrightarrow {NP} = 0 \Rightarrow \overrightarrow {NB} \bot \overrightarrow {NP} \]
NB ⊥ NP.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 Bài 11. Tích vô hướng của hai vectơ có đáp án !!
Copyright © 2021 HOCTAP247
