Cho tam giác ABC có góc A < 90^0. Dựng ra phía ngoài tam giác hai tam giác vuông cân đỉnh A là ABD và ACE. Gọi M, N, P theo thứ tự là trung điểm BC, BD, CE. Chứng minh rằng:Tam

* Hướng dẫn giải

Lời giải

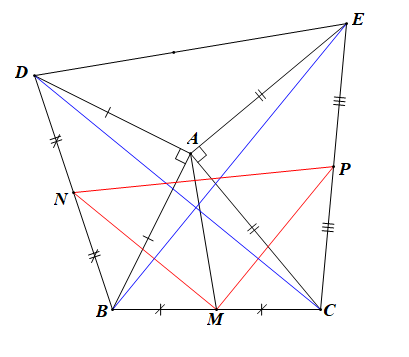
Ta có: \(B{E^2} = {\overrightarrow {BE} ^2} = {\left( {\overrightarrow {AE} - \overrightarrow {AB} } \right)^2}\)

\( = {\overrightarrow {AE} ^2} - 2.\overrightarrow {AE} .\overrightarrow {AB} + {\overrightarrow {AB} ^2}\)

\( = A{E^2} + A{B^2} - 2.AE.AB.cos\widehat {EAB}\)

\[ = A{D^2} + A{C^2} - 2.AD.AC.cos\widehat {CAD}\]

\( = {\overrightarrow {AD} ^2} + {\overrightarrow {AC} ^2} - 2\overrightarrow {AD} .\overrightarrow {AC} \)

\( = {\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right)^2}\)

\( = {\overrightarrow {CD} ^2} = C{D^2}\)

BE = CD(1)

Xét tam giác BCD có M, N lần lượt là trung điểm của BC, BD

Nên MN là đường trung bình của ∆BCD

\( \Rightarrow MN = \frac{1}{2}CD\) và MN // CD(2)

Chứng minh tương tự ta cũng có:

MP là đường trung bình của ∆BCE

\( \Rightarrow MP = \frac{1}{2}BE\) và MP // BE(3)

Từ (1), (2) và (3) suy ra MN = MP.

Vì BE ⊥ CD (câu b), MN // CD và MP // BE

Nên MN ⊥ MP

\( \Rightarrow \widehat {NMP} = 90^\circ \)

Tam giác MNP có MN = MP và \(\widehat {NMP} = 90^\circ \)

Suy ra tam giác MNP là tam giác vuông cân tại M.