Cho hai vectơ a và vecto b thoả mãn | a | = 6, | b | = 8 và | a + b| = 10. Tính số đo của góc giữa hai vectơ a và vecto b

* Hướng dẫn giải

Lời giải

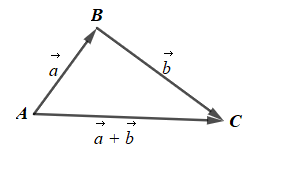
Gọi ba điểm A, B, C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \)

Khi đó \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

Và AB = 6, BC = 8 và AC = 10.

Xét tam giác ABC có:

• AB² + BC² = 6² + 8² =100

AC² = 10² = 100

AB² + BC² = AC²

Do đó tam giác ABC vuông tại B (định lí Pythagore đảo)

• \(cos\widehat {BAC} = \frac{{AB}}{{AC}} = \frac{6}{{10}} = \frac{3}{5}\)

\(cos\left( {\overrightarrow a ;\overrightarrow a + \overrightarrow b } \right) = cos\widehat {BAC} = \frac{3}{5}\)

\[ \Rightarrow \widehat {BAC} \approx 53^\circ 7'48''\]

Vậy \(\left( {\overrightarrow a ;\overrightarrow a + \overrightarrow b } \right) \approx 53^\circ 7'48''.\)