Cho tam giác ABC không cân. Gọi D, E, F theo thứ tự là chân các đường cao kẻ từ A, B, C; gọi M, N, P tương ứng là trung điềm các cạnh BC, CA, AB. Chứng minh rằng ( overrightarrow {...

* Hướng dẫn giải

Lời giải

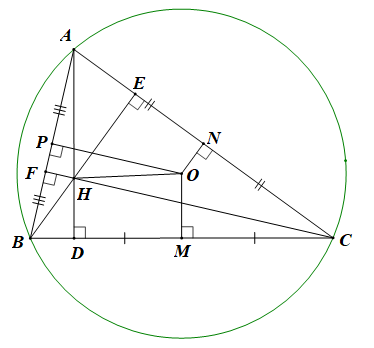
Gọi H và O là tâm đường tròn ngoại tiếp tam giác ABC.

• Vì D, M lần lượt là hình chiếu của H và O lên BC, nên \(\overrightarrow {MD} \) là hình chiếu của \(\overrightarrow {OH} \) trên giá của \(\overrightarrow {BC} \)

Theo định lí hình chiếu (được giới thiệu ở phần Nhận xét của Ví dụ 2, trang 62, Sách Bài tập Toán 10, tập một) ta có:

\(\overrightarrow {OH} .\overrightarrow {BC} = \overrightarrow {MD} .\overrightarrow {BC} \)

\( \Rightarrow \overrightarrow {MD} .\overrightarrow {BC} = \overrightarrow {OH} .\overrightarrow {BC} = \overrightarrow {OH} .\left( {\overrightarrow {OC} - \overrightarrow {OB} } \right)\)

\( \Rightarrow \overrightarrow {MD} .\overrightarrow {BC} = \overrightarrow {OH} .\overrightarrow {OC} - \overrightarrow {OH} .\overrightarrow {OB} \)(1)

Chứng minh tương tự ta cũng có:

• \(\overrightarrow {NE} .\overrightarrow {CA} = \overrightarrow {OH} .\overrightarrow {CA} = \overrightarrow {OH} .\left( {\overrightarrow {OA} - \overrightarrow {OC} } \right)\)

\[ \Rightarrow \overrightarrow {NE} .\overrightarrow {CA} = \overrightarrow {OH} .\overrightarrow {OA} - \overrightarrow {OH} .\overrightarrow {OC} \](2)

• \(\overrightarrow {PF} .\overrightarrow {AB} = \overrightarrow {OH} .\overrightarrow {AB} = \overrightarrow {OH} .\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right)\)

\[ \Rightarrow \overrightarrow {PF} .\overrightarrow {AB} = \overrightarrow {OH} .\overrightarrow {OB} - \overrightarrow {OH} .\overrightarrow {OA} \](3)

Từ (1), (2) và (3) ta có:

\(\overrightarrow {MD} .\overrightarrow {BC} + \overrightarrow {NE} .\overrightarrow {CA} + \overrightarrow {PF} .\overrightarrow {AB} \)

\[ = \overrightarrow {OH} .\overrightarrow {OC} - \overrightarrow {OH} .\overrightarrow {OB} + \overrightarrow {OH} .\overrightarrow {OA} - \overrightarrow {OH} .\overrightarrow {OC} + \overrightarrow {OH} .\overrightarrow {OB} - \overrightarrow {OH} .\overrightarrow {OA} \]

= 0

Vậy \(\overrightarrow {MD} .\overrightarrow {BC} + \overrightarrow {NE} .\overrightarrow {CA} + \overrightarrow {PF} .\overrightarrow {AB} = 0.\)