Trong mặt phẳng toạ độ Oxy cho ba điểm A(–3; 2), B(1; 5) và C(3; −1). Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tìm toạ độ của I.

* Hướng dẫn giải

Lời giải

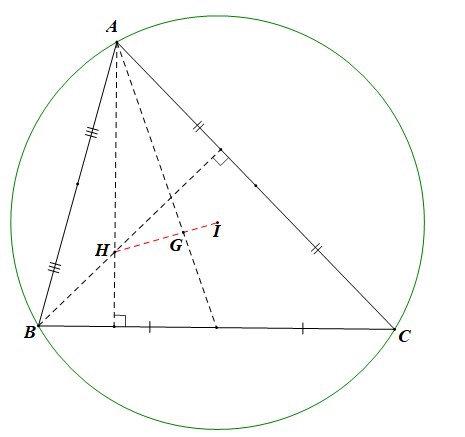
Theo kết quả phần a) của Bài 4.15, trang 54, Sách Bài tập, Toán 10, tập một ta có:

\(\overrightarrow {AH} = 2\overrightarrow {IM} \) với M là trung điểm của BC.

Giả sử I(a; b) là tọa độ tâm đường tròn ngoại tiếp tam giác ABC

Với A(–3; 2), B(1; 5), C(3; −1), H(0; 3) và I(a; b) ta có:

• \(\overrightarrow {AH} = \left( {3;1} \right)\)

• M là trung điểm của BC nên \(\left\{ \begin{array}{l}{x_M} = \frac{{1 + 3}}{2} = 2\\{y_M} = \frac{{5 + \left( { - 1} \right)}}{2} = 2\end{array} \right.\)

M(2; 2)

\( \Rightarrow \overrightarrow {IM} = \left( {2 - a;2 - b} \right)\)

\( \Rightarrow 2\overrightarrow {IM} = \left( {4 - 2a;4 - 2b} \right)\)

Ta có \(\overrightarrow {AH} = 2\overrightarrow {IM} \)

\( \Leftrightarrow \left\{ \begin{array}{l}3 = 4 - 2a\\1 = 4 - 2b\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = \frac{3}{2}\end{array} \right.\) \( \Rightarrow I\left( {\frac{1}{2};\frac{3}{2}} \right)\)

Vậy tọa độ tâm đường tròn ngoại tiếp tam giác ABC là \(I\left( {\frac{1}{2};\frac{3}{2}} \right).\)