Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3km/h. Nếu người chèo...
Câu hỏi :
Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3km/h. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách AH = 300m và gặp người đi bộ tại địa điểm cách B một khoảng BH = 1 400m. Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22).
Tính khoảng cách CB.
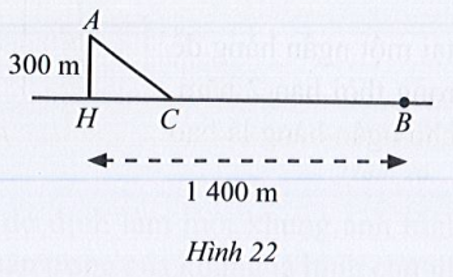
Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3km/h. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách AH = 300m và gặp người đi bộ tại địa điểm cách B một khoảng BH = 1 400m. Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22).
Tính khoảng cách CB.

* Đáp án
* Hướng dẫn giải
Lời giải
Đặt CH = x (x ≥ 0). Khi đó BC = 1 400 – x.
Xét tam giác AHC vuông tại H, có:
AH2 + HC2 = AC2
⇔ AC2 = 3002 + x2
⇔ AC = \(\sqrt {{x^2} + 90\,000} \)
Thời gian thuyền đi từ A đến C là: \(\frac{{\sqrt {{x^2} + 90\,000} }}{3}\) (giờ)
Thời gian người đi bộ đi từ B đến C là \(\frac{{1\,400 - x}}{6}\) (giờ)
Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C nên ta có:
\(\frac{{\sqrt {{x^2} + 90\,000} }}{3} = \,\frac{{1\,400 - x}}{6}\)
⇔ \(2\sqrt {{x^2} + 90\,000} = \,1400 - x\) (điều kiện x ≤ 1 400)
⇔ 4(x2 + 90 000) = 1 960 000 – 2 800x + x2
⇔ 3x2 + 2 800x – 1 600 000 = 0
⇔ x = 400 (TMĐK) hoặc x = \( - \frac{{4000}}{3}\) (không TMĐK)
⇒ CB = 1 400 – x = 1 400 – 400 = 1 000 (m).
Vậy khoảng cách CB = 1 000 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 CD Bài 5. Hai dạng phương trình quy về phương trình bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
