Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Giải SBT Toán 10 CD Bài tập cuối chương 3 có đáp án !!
Vẽ đồ thị của mỗi hàm số sau: y =...
Vẽ đồ thị của mỗi hàm số sau: y = 2x^2 – 8x + 1;
Câu hỏi :
Vẽ đồ thị của mỗi hàm số sau:
y = 2x2 – 8x + 1;
Vẽ đồ thị của mỗi hàm số sau:
y = 2x2 – 8x + 1;
* Đáp án
* Hướng dẫn giải
Lời giải
Xét hàm số y = 2x2 – 8x + 1, có a = 2 > 0, ∆ = (– 8)2 – 4.1.2 = 56 > 0.
- Điểm đỉnh: I = \(\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right) = \left( { - \frac{{ - 8}}{{2.2}}; - \frac{{56}}{{4.2}}} \right) = \left( {2; - 7} \right)\).
- Trục đối xứng là x = 2.
- Vì a = 2 > 0 thì đồ thị hàm số có bề lõm hướng lên trên.
- Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0; 1).
- Điểm đối xứng với điểm (0; 1) qua trục đối xứng là (4; 1).
- Đồ thị cắt trục hoành tại hai điểm có tọa độ \(\left( {\frac{{4 - \sqrt {14} }}{2};0} \right)\) và \(\left( {\frac{{4 + \sqrt {14} }}{2};0} \right)\)
Ta có hình vẽ sau:
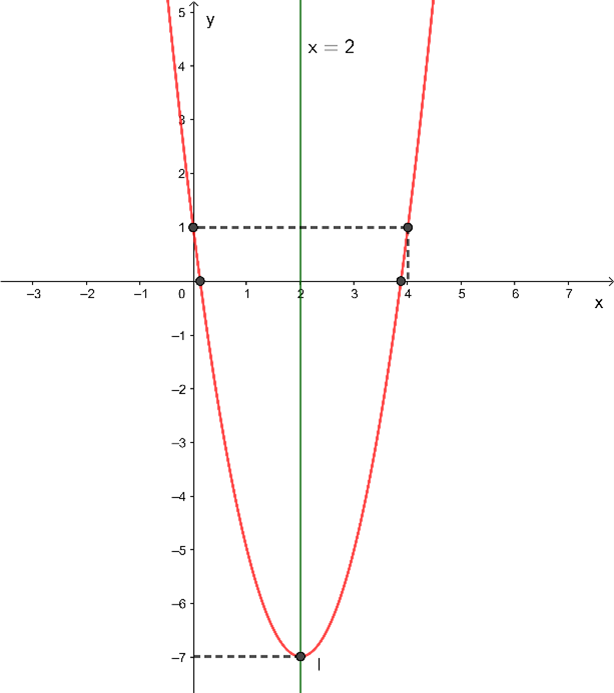
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 CD Bài tập cuối chương 3 có đáp án !!
Số câu hỏi: 23
Copyright © 2021 HOCTAP247
