Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Giải SBT Toán 10 Bài tập cuối chương 1 có đáp án !!
Một lớp học có 36 học sinh, trong đó 20...
Một lớp học có 36 học sinh, trong đó 20 người thích bóng rổ, 14 người thích
Câu hỏi :
Một lớp học có 36 học sinh, trong đó 20 người thích bóng rổ, 14 người thích bóng bàn và 10 người không thích môn nào trong hai môn thể thao này.
Có bao nhiêu học sinh của lớp thích cả hai môn trên?
Một lớp học có 36 học sinh, trong đó 20 người thích bóng rổ, 14 người thích bóng bàn và 10 người không thích môn nào trong hai môn thể thao này.
Có bao nhiêu học sinh của lớp thích cả hai môn trên?
* Đáp án
* Hướng dẫn giải
Kí hiệu A là tập hợp các học sinh của lớp, B = {x ∈ A | x thích bóng rổ},
C = {x ∈ A | x thích bóng bàn}, D = {x ∈ A | x không thích môn nào trong hai môn}.
Theo giả thiết, ta có: n(A) = 36, n(B) = 20, n(C) = 14 và n(D) = 10.
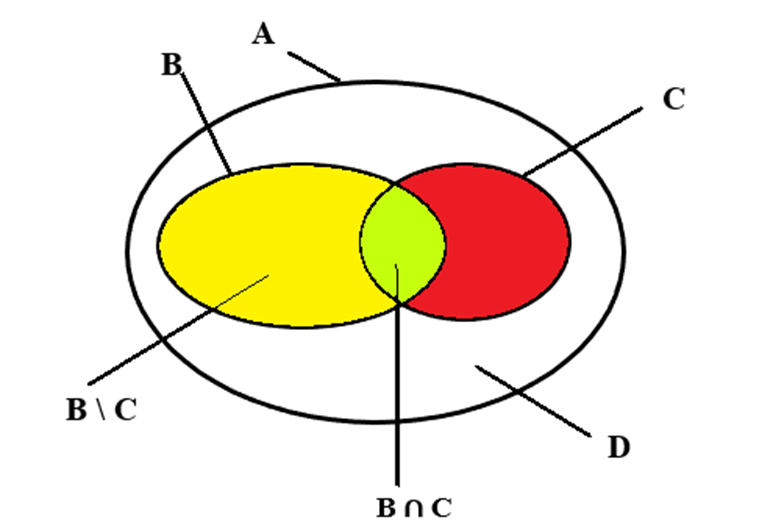
Số học sinh thích một trong hai môn là:
n(B ∪ C) = n(A) – n(D) = 36 – 10 = 26 (bạn).
Số học sinh thích cả hai môn thể thao trên là:
n(B ∩ C) = n(B) + n(C) – n(B ∪ C) = 20 + 14 – 26 = 8 (bạn).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 Bài tập cuối chương 1 có đáp án !!
Số câu hỏi: 51
Copyright © 2021 HOCTAP247
