Một học sinh dự định làm các bình hoa bằng giấy để bán trong một hội

Câu hỏi :

Một học sinh dự định làm các bình hoa bằng giấy để bán trong một hội chợ gây quỹ từ thiện. Cần 1 giờ để làm một bình hoa loại nhỏ và sẽ bán với giá 100 nghìn đồng, 90 phút để làm một bình hoa loại lớn và sẽ bán với giá 200 nghìn đồng. Học sinh này chỉ thu xếp được 15 giờ nghỉ để làm và ban tổ chức yêu cầu phải làm ít nhất là 12 bình hoa. Hãy cho biết bạn ấy cần làm bao nhiêu bình hoa mỗi loại để gây quỹ từ thiện được nhiều tiền nhất.

* Đáp án

* Hướng dẫn giải

Gọi x và y lần lượt là số bình hoa loại nhỏ và loại lớn mà bạn học sinh có thể làm được (x ≥ 0, y ≥ 0).

Đổi 90 phút = 1,5 giờ.

Ban tổ chức yêu cầu phải làm ít nhất 12 bình hoa nên x + y ≥ 12.

Số giờ để làm x bình hoa loại nhỏ là x (giờ), số giờ để làm y bình hoa loại lớn là 1,5y (giờ).

Vì học sinh này chỉ thu xếp được 15 giờ nghỉ để làm nên x + 1,5y ≤ 15.

Do đó, ta có hệ bất phương trình sau: $\left\{\begin{array}{l}x+y\ge 12\\ x+1,5y\le 15\\ x\ge 0\\ y\ge 0\end{array}\right.$

Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tam giác ABC có tọa độ các đỉnh là A(12; 0), B(15; 0), C(6; 6) (phần không gạch chéo kể cả bờ trong hình dưới).

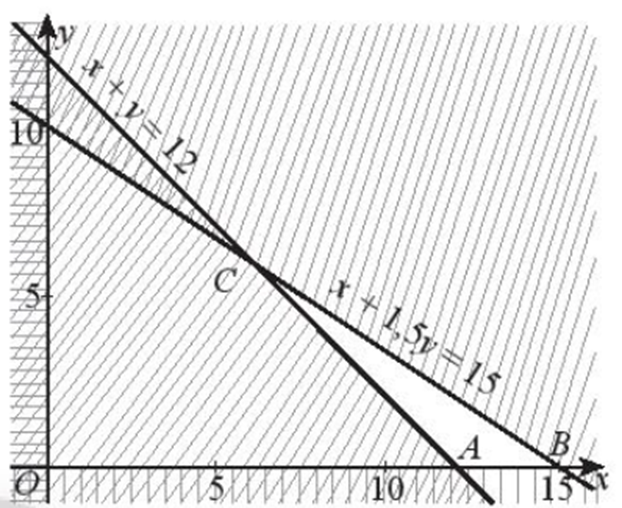
Số tiền gây quỹ là F = 100x + 200y.

Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tam giác ABC.

Ta có: F(12; 0) = 100 . 12 + 200 . 0 = 1 200

F(15; 0) = 100 . 15 + 200 . 0 = 1 500

F(6; 6) = 100 . 6 + 200 . 6 = 1 800.

Do đó, F đạt GTLN là 1 800 nghìn đồng tại đỉnh C(6; 6).

Vậy bạn đó cần làm 6 cái bình hoa mỗi loại để gây được quỹ nhiều tiền nhất.