Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Giải SBT Toán 10 CD Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án !!
Hai người A và B cùng quan sát một con...
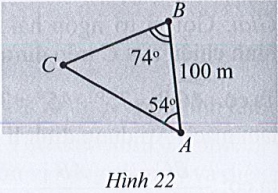
Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C. Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng AB = 100m. Hai người ti...
Câu hỏi :
Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C. Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng AB = 100m. Hai người tiến hành đo đạc và thu được kết quả \(\widehat {CAB} = 54^\circ ,\widehat {CBA} = 74^\circ \)(Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?

* Đáp án
* Hướng dẫn giải
Lời giải
Xét tam giác ABC, có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc)
⇒ \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 180^\circ - \left( {54^\circ + 74^\circ } \right) = 52^\circ \).
Áp dụng định lí sin, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
⇔ \(\frac{{BC}}{{\sin 54^\circ }} = \frac{{100}}{{\sin 52^\circ }}\)
⇔ \(BC = \frac{{100.\sin 54^\circ }}{{\sin 52^\circ }} \approx 102,7\).
Vậy con tàu cách đảo 102, 7 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 CD Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án !!
Số câu hỏi: 16
Copyright © 2021 HOCTAP247
