Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Giải SBT Toán 10 CD Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án !!
Một người đi dọc bờ biển từ vị trí A...
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: AB = 30 m, góc CAB = 60^0 , góc...
Câu hỏi :
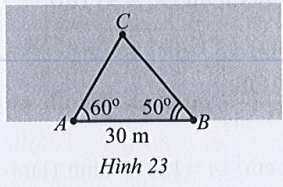
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: AB = 30 m, \(\widehat {CAB} = 60^\circ ,\widehat {CBA} = 50^\circ \) (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

* Đáp án
* Hướng dẫn giải
Lời giải
Xét tam giác ABC, có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc)
⇒ \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 180^\circ - \left( {60^\circ + 50^\circ } \right) = 70^\circ \).
Áp dụng định lí sin, ta được:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
⇔ \(\frac{{30}}{{\sin 70^\circ }} = \frac{{AC}}{{\sin 50^\circ }}\)
⇔ \(AC = \frac{{30.\sin 50^\circ }}{{\sin 70^\circ }} \approx 24,5\)
Vậy khoảng cách từ vị trí A đến con tàu C là 24,5 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 CD Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án !!
Số câu hỏi: 16
Copyright © 2021 HOCTAP247
