Cho hai vectơ a ,cvectơ b khác vectơ 0. Chứng minh rằng nếu hai vectơ cùng hướng thì | vectơ a | + | vectơ b | = | vectơ a + vectơ b |

* Hướng dẫn giải

Lời giải

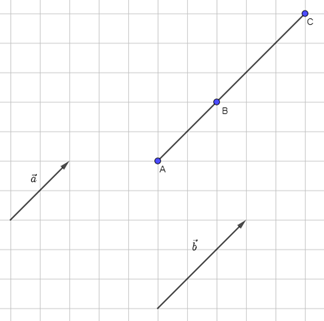
Không mất tính tổng quát ta lấy một điểm A bất kì, vẽ \(\overrightarrow {AB} = \overrightarrow a \), \(\overrightarrow {BC} = \overrightarrow b \)

Vì hai vectơ \(\overrightarrow a ,\overrightarrow b \) cùng hướng nên A, B, C thẳng hàng, B nằm giữa A và C.

Ta có: \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow {AB} } \right| = AB,\left| {\overrightarrow b } \right| = \left| {\overrightarrow {BC} } \right| = BC\)

⇒ \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = AB + BC = AC\)

\( \Rightarrow \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow {AB} + \overrightarrow {BC} } \right| = \overrightarrow {AC} \).

Vậy \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\).