Cho hình vuông ABCD cạnh a. Tính | vecto AB + vecto AC|

* Hướng dẫn giải

Lời giải

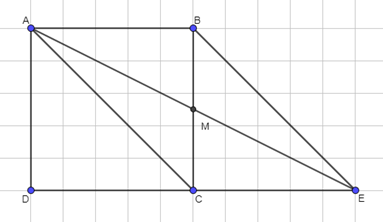
Lấy E là điểm thỏa mãn ABEC là hình bình hành, gọi M là trung điểm của BC.

Khi đó ta có:

\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AE} \)

⇒ \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AE} } \right| = AE\)

Vì M là trung điểm của BC nên M là trung điểm của AE

⇒ AE = 2AM.

Xét tam giác ABM vuông tại B, có:

AM² = AB² + BM² (định lí pythagoras)

⇔ AM² = a² + \({\left( {\frac{a}{2}} \right)^2}\)= a² + \(\frac{{{a^2}}}{4}\) = \(\frac{{5{a^2}}}{4}\)

⇔ AM = \(\frac{{\sqrt 5 a}}{2}\)

⇒ AE = 2AM = \(2.\frac{{\sqrt 5 a}}{2} = \sqrt 5 a\)

Vậy AE = \(\sqrt 5 a\).