Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo, E là trung điểm của AD, G là giao điểm của BE và AC. Tính: vecto OA + vecto OB + vecto OC + vecto OD

Lời giải

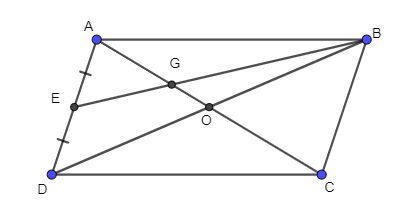
Xét hình bình hành ABCD, có O là giao điểm của AC và BD nên O là trung điểm của AC và O là trung điểm của BD.

⇒ \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \) và \(\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \)

Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)

\( = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right)\)

\( = \overrightarrow 0 + \overrightarrow 0 \)

\( = \overrightarrow 0 \).

Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).