Cho tam giác ABC đều cạnh a. Các điểm M, N lần lượt thuộc các tia BC và CA thỏa mãn BM = 1/3BC, CN = 5/4CA. Tính: vecto AB . vecto AC , vecto AM . vecto BN

Lời giải

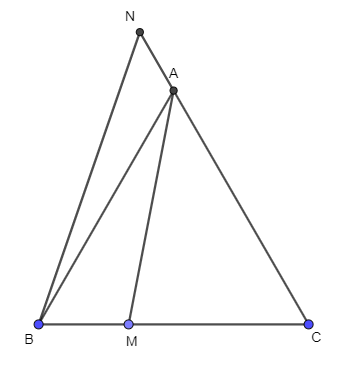
 Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.cos\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)

= \(AB.AC.\cos \widehat {BAC}\)

= \(a.a.\cos 60^\circ \)

= \(\frac{1}{2}{a^2}\)

\(\overrightarrow {AM} .\overrightarrow {BN} = \left( {\overrightarrow {AB} + \overrightarrow {BM} } \right).\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)

\( = \left( {\overrightarrow {AB} + \frac{1}{3}\overrightarrow {BC} } \right).\left( {\frac{1}{4}\overrightarrow {CA} - \overrightarrow {AB} } \right)\)

\( = \left[ {\overrightarrow {AB} + \frac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)} \right].\left( { - \frac{1}{4}\overrightarrow {AC} - \overrightarrow {AB} } \right)\)

\( = \left( {\frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right).\left( { - \frac{1}{4}\overrightarrow {AC} - \overrightarrow {AB} } \right)\)

\( = - \frac{2}{3}\overrightarrow {AB} .\frac{1}{4}\overrightarrow {AC} - \frac{2}{3}\overrightarrow {AB} .\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} .\frac{1}{4}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AC} .\overrightarrow {AB} \)

\( = - \frac{1}{6}\overrightarrow {AB} .\overrightarrow {AC} - \frac{2}{3}{\overrightarrow {AB} ^2} - \frac{1}{{12}}{\overrightarrow {AC} ^2} - \frac{1}{3}\overrightarrow {AC} .\overrightarrow {AB} \)

\( = - \frac{1}{6}.\frac{1}{2}{a^2} - \frac{2}{3}.{a^2} - \frac{1}{{12}}.{a^2} - \frac{1}{3}.\frac{1}{2}{a^2}\)

\( = - \frac{1}{{12}}{a^2} - \frac{2}{3}.{a^2} - \frac{1}{{12}}.{a^2} - \frac{1}{6}{a^2}\)

\( = - {a^2}\).