Tìm các giá trị lượng giác của góc 120°.

* Hướng dẫn giải

Hướng dẫn giải:

Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = 120^\circ \).

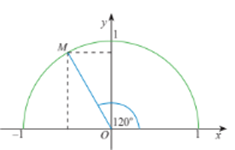Ta có: \(\widehat {MOy} = 120^\circ - 90^\circ = 30^\circ \).

Ta tính được tọa độ điểm M: \(\left\{ \begin{array}{l}{x_0} = - \left( {OM.\sin 30^\circ } \right) = - \left( {1.\frac{1}{2}} \right) = - \frac{1}{2}\\{y_0} = OM.\cos 30^\circ = 1.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\end{array} \right.\).

Hay \(M\left( { - \frac{1}{2};\,\,\frac{{\sqrt 3 }}{2}} \right)\).

Vậy theo định nghĩa ta có:

\(\sin 120^\circ = \frac{{\sqrt 3 }}{2};\,\cos 120^\circ = - \frac{1}{2}\); \(\tan 120^\circ = - \sqrt 3 ;\,\cot 120^\circ = - \frac{{\sqrt 3 }}{3}\).